希望通过本篇文章，能够帮助产品经理对区块链技术有所了解。

最近一年，我一直在关注基于区块链技术的加密数字货币——比如「比特币」、「以太坊」等，并且我认为虽然「加密数字货币」可能因为会威胁（各国）央行的地位而无法发挥更大的作用，但是其底层的支持技术（区块链）可能会改变互联网的形态（至少对于互金领域来说）。

所以一年来我一直在和我司的程序员小哥摸索学习区块链技术，我将在之后的文章里逐步整理和分享基于「以太坊」（Ethereum）的私有区块链网络，实现智能合约的笔记。

但是我想说的是，这并不是一个给程序员小哥来看的开发文章，而是希望能够让一个产品经理对区块链技术有所了解。因为这个系列不会特别深入的去将其中的编程原理，更多是一些基础性的概念。

什么是区块链？

说到区块链，我们一般都会想到以「比特币」为代表的加密数字货币。所以我们就通过「比特币」网络是如何工作的来理解区块链。

就目前的金融情况而言，我们如果进行转账需要找到一个可以信任的第三方（比如银行或第三方支付公司），由这些可信任的第三方来确保交易的有效性，但可信任第三方的存在在一定程度上增加了交易的成本。而基于加密数字货币可以在交易中摒弃可信任的第三方，让任意两人直接的交易成为可能。

比特币交易如何进行

有一个很著名的 Alice 与 Bob 的转账故事来讲清楚比特币交易的运转过程，我就将其简化一下，注意斜体字部分：

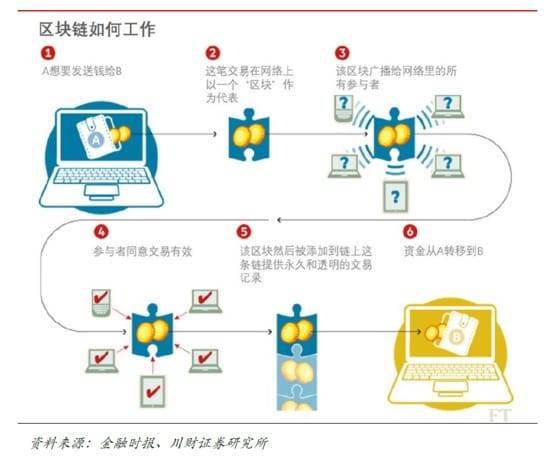
1. Alice 想将一些钱（假设是1 btc）转账给 Bob。
2. Alice 通过基于 P2P 技术（这里的 P2P 可不是网络借贷，而是点对点网络，就是快播用的那个技术）的比特币网络向 Bob 发起比特币转账。这里他们必须想网络提供基于密码学（非对称加密算法）的加密证明（也就是密钥）来证明他们的身份。
3. Alice 与 Bob 的交易记录会被记录在一个「区块」（「block」）中，并且这个「区块」会被通知给比特币网络中其它的节点进行确认。
4. 在比特币网络中的其它节点通过计算一个「难计算、易验证」的数学问题来完成验证。节点验证的动机是因为转账手续费以及在验证过程中新产生的比特币作为找到新块的奖励。在比特币网络中，块的验证被称为「挖矿」。
5. 比特币网络中的每个节点都将会保留之前验证过的所有这些交易的账本副本（分布式记账）：同周期内的交易组成「区块」，按照时间顺序区块会连成链，即「区块链」，从而形成「交易」——>「区块」——>「区块链」的三层结构。
6. 一旦网络中有一个节点解决了之前提到的「难计算、易验证」的数学问题，交易即被确认。新得到的确认的「区块」就会被解决问题的节点添加到这个区块链中，并向网络内其它节点广播。
7. 接下来，网络内的其它节点将验证解决问题的节点的广播（数学问题），并达成共识，即交易成功，并且各节点都已经收到。一旦达成共识，每个节点都将更新各自的交易记录副本。
8. 这时候，区块链的特性开始展现，因为「账本副本」会存在于网络中的每一个节点，理论上任何记录都是
   公开的、不可修改的。试图伪造的交易将无法通过网络内节点的验证,其形成的「区块」将被舍弃。
9. 当完成以上所有步骤后，Alice 的比特币账户余额将减少1 btc，Bob 的余额中讲增加 1 btc.

上边说到了几个词语，需要解释一下：

点对点网络（P2P 网络）

P2P 网络并不是一个新出现的技术，又叫「对等网络」。在这个网络环境中，没有中心服务器，依托用户群交换信息。每个参与者的地位处于平等地位，并没有主从之分。每个参与者既是服务的提供者（server）,也是服务的获取这（client）。和我们生活最贴近的就是媒体播放了。下图为 P2P 网络示意图：

非对称加密算法与加密证明

我们都说比特币是匿名的，但是按照上文提到「比特币交易步骤」，还是需要去证明他们的身份，那么是如何确保「匿名性」的呢？

在比特币网络中，身份（钱包地址）并不是和姓名或者其它的信息对应的，身份（钱包地址）只简单关联一个根据「非对称加密算法」来随机生成的公有/私有密钥(key)。钱包里的钱属于掌握这个私有密钥（key）并可以使用私有密钥（key） 来确认交易的人。使用私有密钥（key） 来确认交易同样不需要姓名或者其他的信息。
一个比特币钱包地址就是一个公钥Key，它是一串由数字和字母组成的「乱码」，比如1A2SH4r5z1gufQw7cj9aLunWhYRyTDbRFW

这就要说到「非对称加密算法」，如果直接搬 Wikipedia 上的讲解会比较枯燥，我们接着举栗子：我用化名写了一本书，这本书非常受欢迎。现在有个人冒充我，自称他是真的「张小璋」，我们叫他「小璋 A」所有的东西都是他写的。那我应该如何来证明呢？

这时我们就可以采用「非对称加密算法」来帮助我们解决这个问题：在书籍出版前我利用非对称加密技术生成了一个密钥对（公/私密钥）并将公钥声明在书中，任何人都可以使用公钥来加密我书中的任意一段文字。谁能将其解密就可以证明谁是这本书的作者。因为「非对称加密算法」公钥用来加密，但只有使用私钥才能够进行解密。「小璋 A」无法对该段文字进行解密，而我可以。这就证明了我是本书的作者，却从未透露你的个人身份。当然，如果我丢了私钥或者「小璋 A」通过其他手段获得了密钥（比如威胁我交出密钥）这不在我们的讨论范围了。

比特币网络并没有限制每个节点生成「钱包地址」的数量，你可以尽情的生成足够过的「钱包地址」从而实现身份匿名的。同时只需要确保正确的密钥来确认交易，既可以完成比特币网络交易的验证。

什么是「区块」

上文提到：区块链网络是由「交易」——>「区块」——>「区块链」的三层结构组成，每个添加到「区块链」上的「区块」都永久记录了交易的数据。

每个区块链都会包含以下内容：

• 上一个区块链的 hash 散列，既可以实现区块的链连接也也可以防止篡改。毕竟理论上不同内容但是出现同一 hash 散列值的可能性比外星人明天入侵地球还要小。
• 随机数，即之前提到的「难计算、易验证」的数学问题的解。这个随机数可以用来其它节点对交易进行验证，同时这个随机数对于每一个区块来说都是独一无二的。
• 交易记录和时间戳。

显然，如果没有「随机数」或者「随机数」被其它节点验证是错误的，新的区块将不会被提交到「链」上，因此「挖矿」的过程本质上是在「求数学解」的过程，目前这个过程一般为10分钟。

共识机制及分布式记账

先说「共识机制」，在比特币网络中采用的是 PoW 算法（即工作量证明），简单来说就是多劳多得。节点（矿工）通过依赖专门的机器（矿机）来进行数学运算获得记账权。谁解决了那个「难计算、易验证」的数学问题，谁就可以得到网络上新产生的比特币和 Alice 在转账过程中要付出的交易费用。同时，获得记账权的节点会向网络中其它的节点宣布新的区块链（旧的区块链加上新的区块）的主张，网络上其它的节点通过检查这个主张（验证随机数）来确认其有效性。

确认完成后（比如7个节点确认，或者10个节点确认），这个主张将会被同步到该网络中所有的网络节点中，同时，该区块链上的所有交易都可以追溯到第一个「创世」区块。因此交易是不可篡改的（任何试图篡改交易的行为会被整个网络上的节点检测到并被因为验证失败而被抛弃）。这也意味着区块链上的数据操作与传统数据库操作不一样：传统数据库我们讲的是「增删改查」，但在区块链上只有「增查」两项，一旦数据记录你将无法编辑（改）或者删除这条数据。

好了，文字写的也不少了，基本上包含了区块链的基础知识，如果你想更深入的了解，我推荐你读一下中本聪关于比特币机制的论文。（如果你读到这里了，就不要问我中本聪是谁……O(∩_∩)O~）

#专栏作家#

张小璋，公众号：张小璋的碎碎念（ID：SylvainZhang），人人都是产品经理专栏作家。野蛮生长的产品经理，专注于互联网金融领域。

本文原创发布于人人都是产品经理。未经许可，禁止转载。

题图来自unsplash，基于CC0协议