在广告拍卖里，它不能保证每次竞拍使得拍卖者的收益最大化，现在我们来探讨下如何选择机制才能使得每次收益最大化，这种机制被称为最优机制。

拍卖有两个目标：卖者收益和社会效用，不同目标决定选择不同的机制，不同机制导致了竞拍人获得物品的不同概率函数和期望支付，以及该机制下的特性，比如激励兼容、个人理性预算平衡等。

在广告系列，机制设计里我们说到在直接机制中，满足激励兼容特性的机制鼓励广告主说真话（b=v）是一个弱占有策略（U≥U’），会形成一个真实均衡，广告主会持续参与竞价，有利于广告生态的长期发展。

但有个现象：它不能保证每次竞拍使得拍卖者的收益最大化，现在我们来探讨下如何选择机制才能使得每次收益最大化，这种机制被称为最优机制。

假设条件不变：

一个不可分割的单品拍卖，潜在买家数量为  ，买家  对物品的估价为  （假设买家知道拍卖品对自己的价值，不受其他买家影响，称为私有价值），卖家不知道买家的真实估值，但知道买家估价的累计分布函数  ,及连续密度函数  ，  相互独立，假设  的范围  ，  。

现在构造一个估价V的函数如下：

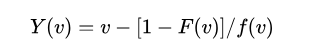
称为买家的虚拟估价函数，假设Y是关于V的递增函数，此时我们称之为常规问题。

分配规则：

价高者得，此时的价指买家虚拟估价的价格，即把拍卖品分配给虚拟估价最高的竞拍者。因为没有假设买家是对称的，所以不同买家有不同的虚拟估价函数，不同函数的斜率可能不同，估价最高的买家虚拟估价不一定是最高的，所以说在最优机制下的拍卖不是一个公平的机制。

支付规则：

二价结算，假设买家  的虚拟估价最高，那么此时买家  的支付为： 。
其中  是买家  虚拟估价函数的反函数， 是除买家  以外虚拟估价最高者，称该机制是不带保留价的最优机制。

下面我们用具体图形展示会更加直观，假设有两个买家1和买家2，虚拟估价函数分别如下所示，当他们的估价分别是  时，买家1的估价函数斜率更大，函数对估价的变动更敏感，则 。

如下图所示：

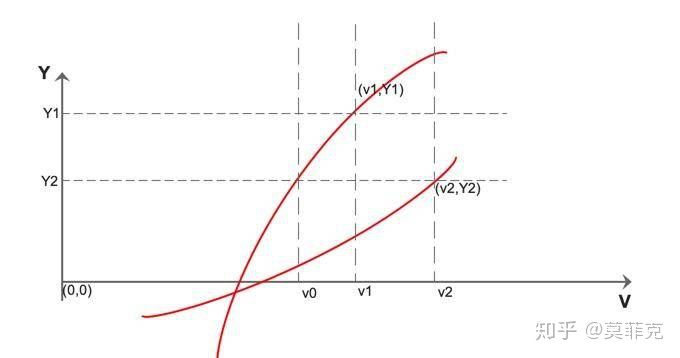
对于广告系统而言，广告主1的支付价格不是，因为广告是按照ECPM来竞价的，我们现在反推一下竞价胜出的广告主应该支付的实际价格，假设按照点击计费（cpc），pCTR是预估点击率，那么买家 i 的竞价值为：

买家2的竞价值为：

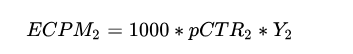
假设  ，则买家1获得该次曝光，买家1的点击支付的实际价格为：

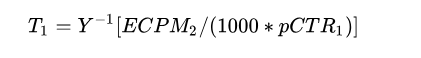
其中，  是买家1虚拟估价的反函数。

广告的实际计费的计算虽然多了一步，但是本质没变，从上图1中我们可以看出，买家2的估价更高但是物品被分配给了买家1，显然不是一个公平的竞价环境，也不是一个有效的拍卖，这涉及到了价格歧视。

看人下菜碟，知道你是个有钱的主，你要同样的东西就得比别人多出钱，怎么知道你是个有钱的？

这就基于系统对你过往的理解，历史数据的收集，通过建模拟合出来你的估价分布函数，有些大数据杀熟的意思，直觉上给人感觉很不公平，不过在现实生活中价格歧视无处不在。

比如工业用电和居民用电价格就不同（三级歧视），出租车分公里数阶梯计费以及个人税分阶梯计费（二级歧视），垄断厂商不同买者不同价格（一级歧视）比比皆是，可是为什么采用虚拟估价函数的时候卖者的收益就最大化了呢，这涉及到经济学的一个解释，我们下节聊。

本文由 @莫菲克 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议