K-means聚类算法:用“物以类聚”的思路挖掘高价值用户
2023年AI产品这么火,连带着相关的行业、技术也变得越发炙热。之前我们已经学习了一些算法,这篇文章,我们来学习聚类问题中最经典的K均值(K-means)算法。

前面的文章中,我们已经学习了K近邻、朴素贝叶斯、逻辑回归、决策树和支持向量机等分类算法,也学习了线性回归等回归算法,其中决策树和随机森林也可以解决回归问题。
今天我们来学习聚类问题中最经典的K均值(K-means)算法,与前面学习过的算法不同的是,聚类算法属于无监督学习,不需要提前给数据的类别打标。
一、基本原理
假设有一个新开办的大学,即便还没有开设任何的社团,有不同兴趣爱好的同学们依然会不自觉的很快聚在一起,比如喜欢打篮球的、喜欢打乒乓球的、喜欢音乐的等等。
这时候就可以顺势开设篮球社团、乒乓球社团、音乐社团,再有同学想加入社团的时候,就可以直接根据自身兴趣选择社团了。
把这个场景迁移到机器学习上,拥有不同兴趣的学生就是数据样本,我们来试着来给他们归类。
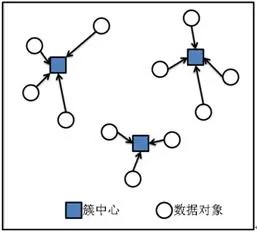
向量空间中,距离近的样本意味着有更高的相似度,我们就把它们归为一类,然后用该类型所有样本的中心位置标识这个类别,再有新样本进来的时候,新样本离哪个类别的中心点更近,就属于哪个类别,然后再重新计算确定新的中心点。
不断重复上述操作,就能把所有的数据样本分成一个个无交集的簇,也就是对所有数据样本完成了归类。
这就是K-means算法的思路:根据距离公式计算n个样本点的距离,距离越近越相似,然后按这个规则把它们划分到K个类别中,让每个类别中的样本点都是更相似的。
我们把这K个类别叫做“聚类”,聚类的表现就是图中一组一组聚在一起的数据,“聚类”的中心位置叫做“质心”,质心代表了聚类内样本的均值。
需要注意的是,K-means算法中的K表示要分成K个聚类,那么如何确定K值就是一个绕不开的问题了。
其实没有统一的标准,我们一般根据个人经验来设定K值,也可以选几个有代表性的K值,然后选择效果最好结果对应的K值即可。
二、应用场景
电商业务中,精细化运营的前提是对用户进行分层,然后根据不同层次的用户采取不同的运营策略。
这时候可以收集用户的消费频率、消费金额、最近消费时间等消费数据,并使用K-means算法将用户分为不同的层级,然后针对高价值用户,可以提供专享活动或个性化服务,提高用户价值感和忠诚度,针对将要流失的用户,可以采用发放优惠券等挽留策略,尽可能留住用户。
K-means算法是一种非常常见的无监督学习算法,以下是一些应用场景:
- 客户细分:在市场营销中,可对客户进行细分,将相似的客户分为同一类,以便进行更有效的营销策略制定。
- 图像分割:在计算机视觉中,可用于图像分割,将图像中的像素分为几个不同的区域。
- 异常检测:可用于异常检测,通过将数据点聚类,找出那些与大多数数据点不同的异常数据点。
- 文档聚类:在自然语言处理中,可用于文档聚类,将相似的文档分为同一类,以便进行更有效的信息检索。
- 社交网络分析:在社交网络分析中,K-means可用于发现社区结构,将相似的用户分为同一类。
三、优缺点
K-means算法的优点:
- 简单易实现:原理简单,实现起来相对容易。
- 计算效率高:时间复杂度近似为线性,对于大规模数据集可以较快地得到结果。
- 可解释性强:结果(即聚类中心)具有很好的可解释性。
K-means算法的缺点:
- 需要预设聚类数目:需要预先设定K值(即聚类的数目),但这个值通常难以准确估计。
- 对初始值敏感:算法结果可能会受到初始聚类中心选择的影响,不同的初始值可能会导致不同的聚类结果。
- 可能收敛到局部最优:可能会收敛到局部最优解,而非全局最优解。
- 对噪声和离群点敏感:对噪声和离群点敏感,这些点可能会影响聚类中心的计算。
四、总结
本文我们介绍了K-means聚类算法,它是一种无监督学习方法,其基本思想是通过计算样本点之间的距离,将距离近的样本归为一类。
尽管K-means算法简单易实现、计算效率高且结果具有很好的可解释性,但它也存在一些缺点,如需要预设聚类数目、对初始值敏感等。因此,在使用K-means算法时,需要根据具体的应用场景和数据特性,适当调整算法参数和处理方式,以达到最佳的聚类效果。
至此,常见的机器学习算法基本介绍完毕,接下来我们开始深度学习算法的学习。
下篇文章,我们会介绍神经网络,神经网络是理解深度学习的基础,敬请期待。
本文由 @AI小当家 原创发布于人人都是产品经理,未经许可,禁止转载
题图来自 Unsplash,基于 CC0 协议
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务。
- 目前还没评论,等你发挥!


 起点课堂会员权益
起点课堂会员权益







