在数据分析和决策支持领域，回归模型是解决复杂业务问题的强大工具。本文通过深入探讨回归模型在预测和解释变量关系中的应用，展示了如何利用多元线性回归和逻辑回归模型解决实际业务中的决策问题

在上一篇deepseek生成时间预测模型分析之后，继续探索deepseek结合分析的可能性，让它用于解决业务中常见的决策问题。

常见决策问题

预测问题：已知一部分变量，想要预测另一变量。

• 比较常见的，比如在知道二手房房屋面积、房龄、地段、房屋新旧程度等因素，想要知道它的售卖价格应该定在多少；
• 又或者知道一个人的收入水平、年龄、性别、历史信用卡还款及时情况、近期消费金额，想要知道这个人对一笔大额借款的借款概率和违约概率是多少，是借款优质用户，还是违约高危用户？

解释：在众多变量中，想要知道这些变量对目标变量的影响程度是多大。

• 比如在房屋面积、房龄、地段、房屋新旧程度，哪个是对房屋价格影响最大的因素，在重点获得房源时，应该着重关注哪个？
• 又或者收入水平、年龄、性别、历史信用卡还款及时情况、近期消费金额等对判断优质/高危的人群，哪个是更重要的因素，在扩展用户中应该重点关注哪部分用户？

回归模型简介

以上两个问题，使用多元线性模型和逻辑回归模型可简单解决。

B端产品经理的能力模型与学习提升

B端产品经理面临的第一大挑战，是如何正确的分析诊断业务问题。 这也是最难的部分，产品设计知识对这部分工作基本没有帮助，如果想做好业务分析诊断，必须具备扎实 ...

查看详情 >

简单看一下两个模型的数学表达式：

1. 线性回归：Y=β0+β1X1+β2X2+β3X3+···+βkXk
2. 逻辑回归：ln(P/(1-P))=β0+β1X1+β2X2+β3X3+···+βkXk ，进行指数转化即可得到概率公式

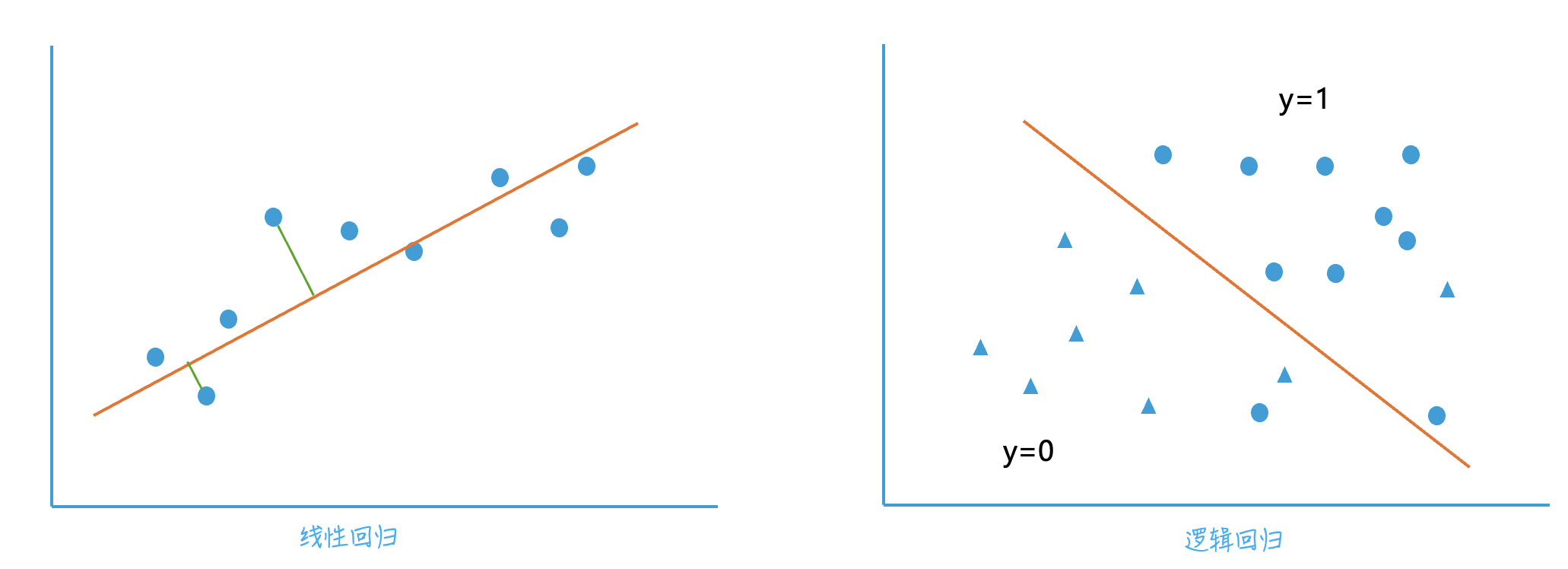
其中X为变量，β为参数，以示意图来理解的话（非数学表达式对应图形）

简单解释上图：多元线性回归，就是找到一条线，使得每组x对应的预测值y都与真实y距离和最短（垂直距离）;逻辑回归，是找到一条线，可以将两个不同的类别，准确分到这条线的两边，与实际类别相比预测对的个数越多越好。

逻辑回归其实是一种特殊的多元线性回归，它进行了一次指数转化，把线性回归结果值映射到(0,1]上并保持单调，表达的含义为是y的概率，如以会流失的用户为目标群体，所计算的概率就为用户流失率。

回归模型案例实操

举个例子做个实操，假如在二手车交易平台，新上架一辆二手车，现在需要填写参考价格，希望它既能很快卖掉，又可以尽量多赚到钱。

先梳理一下报价的参考信息，车辆的参数很多如发动机相关的排量、智能系统是否有中控屏、车辆辅助配置是否有雷达等，这些同新车参数一样，也有一些二手车特有比如行驶里程、上牌年份等。重点挑一下对购买具有决策价值的字段，假如筛了如下这些：

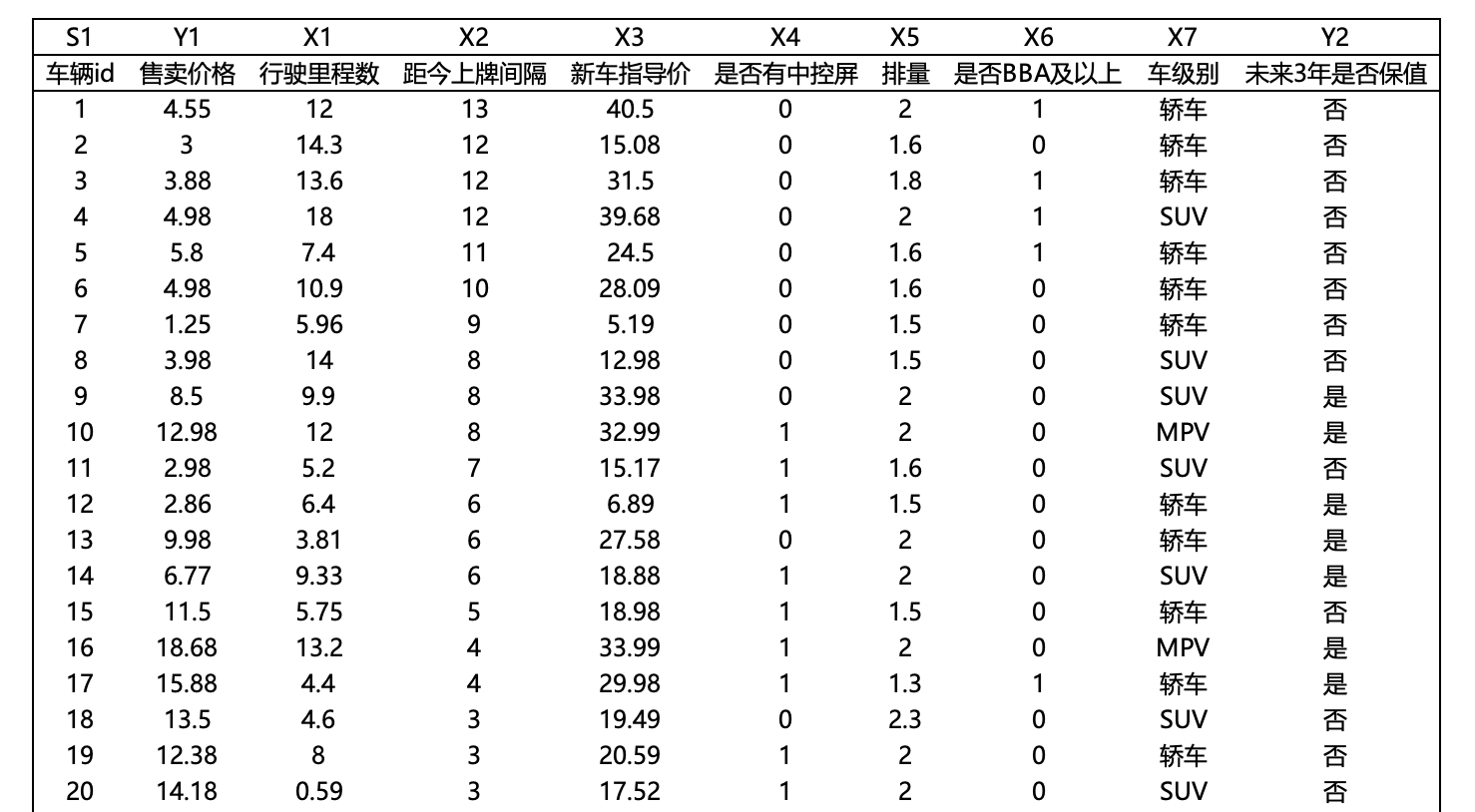
对于二手车预计价格可以用多元线性回归模型处理，对于未来3年是否保值这类是否问题，可以使用逻辑回归预测未来3年可保值(p>0.5)的概率。模型选择之后，可能还需要解决一些疑问：

1. 自变量的处理

• 年份，它本身是个数值，但该数值并没有任何物理含义，需要加工一下让它变成距离今天的时间间隔，年份越小，车子越新。
• 排量，它是能衡量发动机性能具有物理含义的指标，但多数情况下车的排量只有几档，数值本身作用不大，需要对它进行效应编码，提取它的序1、2、3、4。
• 车级别、是否有中控屏或是否BBA等，甚至连数字都不是，很难放到线性模型里，这时就需要对类别做处理生成虚拟变量，比如以车辆类别的“轿车”作为参考组，SUV和MPV表示如下

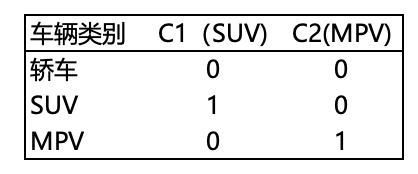
2. 参数估计

• 线性回归，通过计算预估值和真实值最小均方误差，MSE = (1/n) * Σ(y_i – ŷ_i)^2，其中n是样本数量，y_i是真实值，ŷ_i是预测值，数值越小误差越小。
• 逻辑回归，通过最小化对数损失 Log Loss = – (1/N) * Σ [y_i * log(p_i) + (1 – y_i) * log(1 – p_i)]，log loss越小表示损失越小。

3. 模型评估指标

• 线性回归，R2、MSE、调整R2 ，R2越高越好，MSE越低越好。
• 逻辑回归，准确率、AUC-ROC、混淆矩阵、F1分数，AUC越高越好。

4. 模型结果

【二手车价格预测模型】

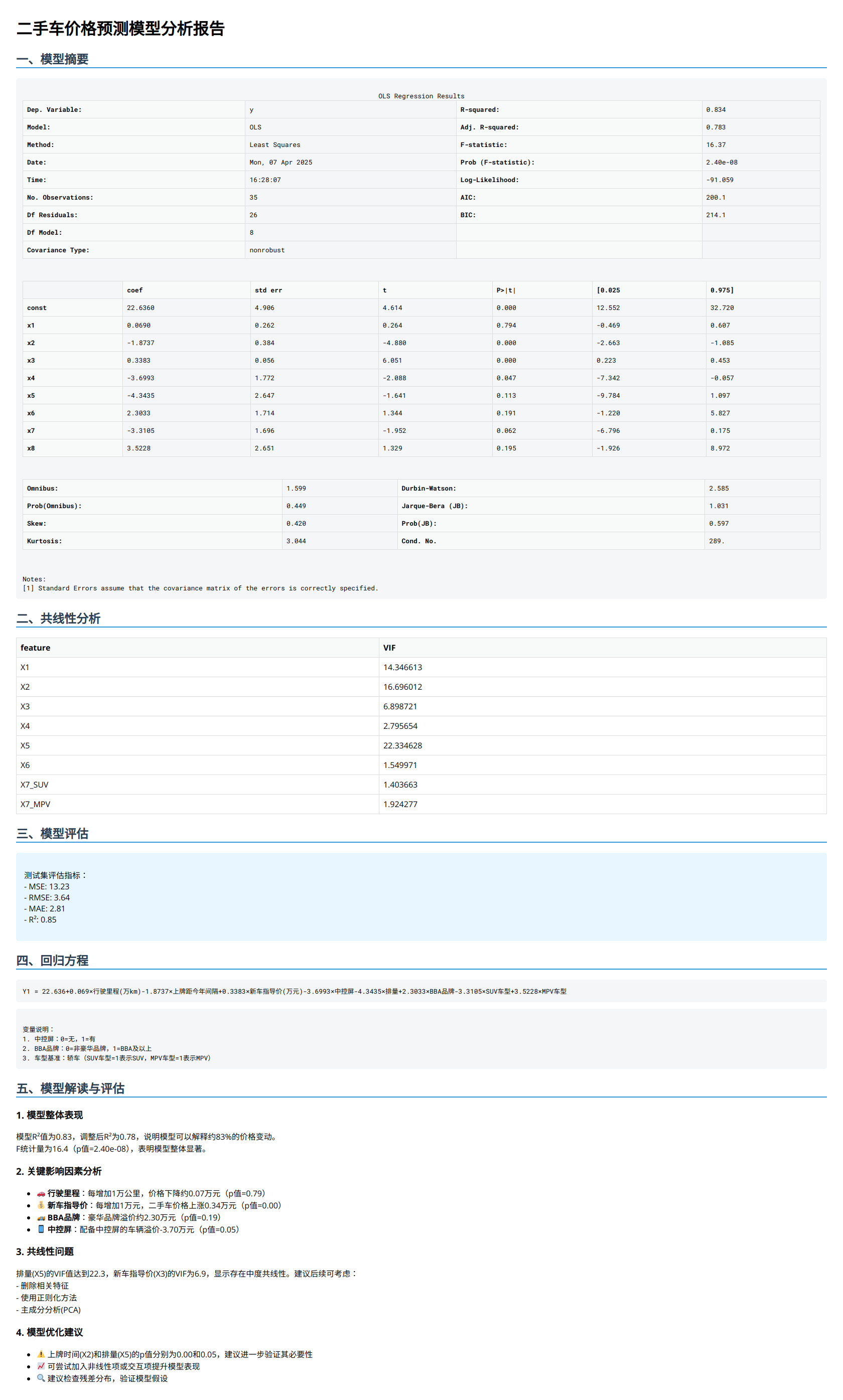
价格预测模型公式 Y1 = 22.636+0.069×行驶里程(万km)-1.8737×上牌距今年间隔+0.3383×新车指导价(万元)-3.6993×中控屏-4.3435×排量+2.3033×BBA品牌-3.3105×SUV车型+3.5228×MPV车型

假如新上架一辆二手车，对应的变量如下，求Y1

• X1 行驶里程数：12
• X2 距今上牌年份间隔：6
• X3 新车指导价：29.75
• X4 是否有中控屏：1
• X5 排量：2
• X6 是否BBA及以上：0
• X7 SUV车型：0
• X8 MPV车型：0

预测：可通过变量进行二手车售卖价格为9.89万元

模型解释：

• 回看公式，以X2和X3 这两个系数较为显著的变量来看，X2距今上牌间隔车龄每增加一年，价格就会下降1.87万；而X3新车指导价每增加1万元，对于二手车价格就会增加0.3万元（其他变量是均值的情况下）
• 而对于X7和X8来说，是在车级别为轿车的基础上判断对二手车价格的影响，即相对于轿车而言，如果是SUV则二手车价格会降3万元，如果是MPV则会增加3.5万元（当然这里的P值不显著即该变量其实对结果影响并没有那么大）
• 还要注意的是，这里通过VIF分析和经验判断，也会发现一点问题，即行驶里程和上牌距今年间隔具有很强的相关性，且X2 VIF=16.69，需要做特征选择或变换。

【二手车是否保值模型】

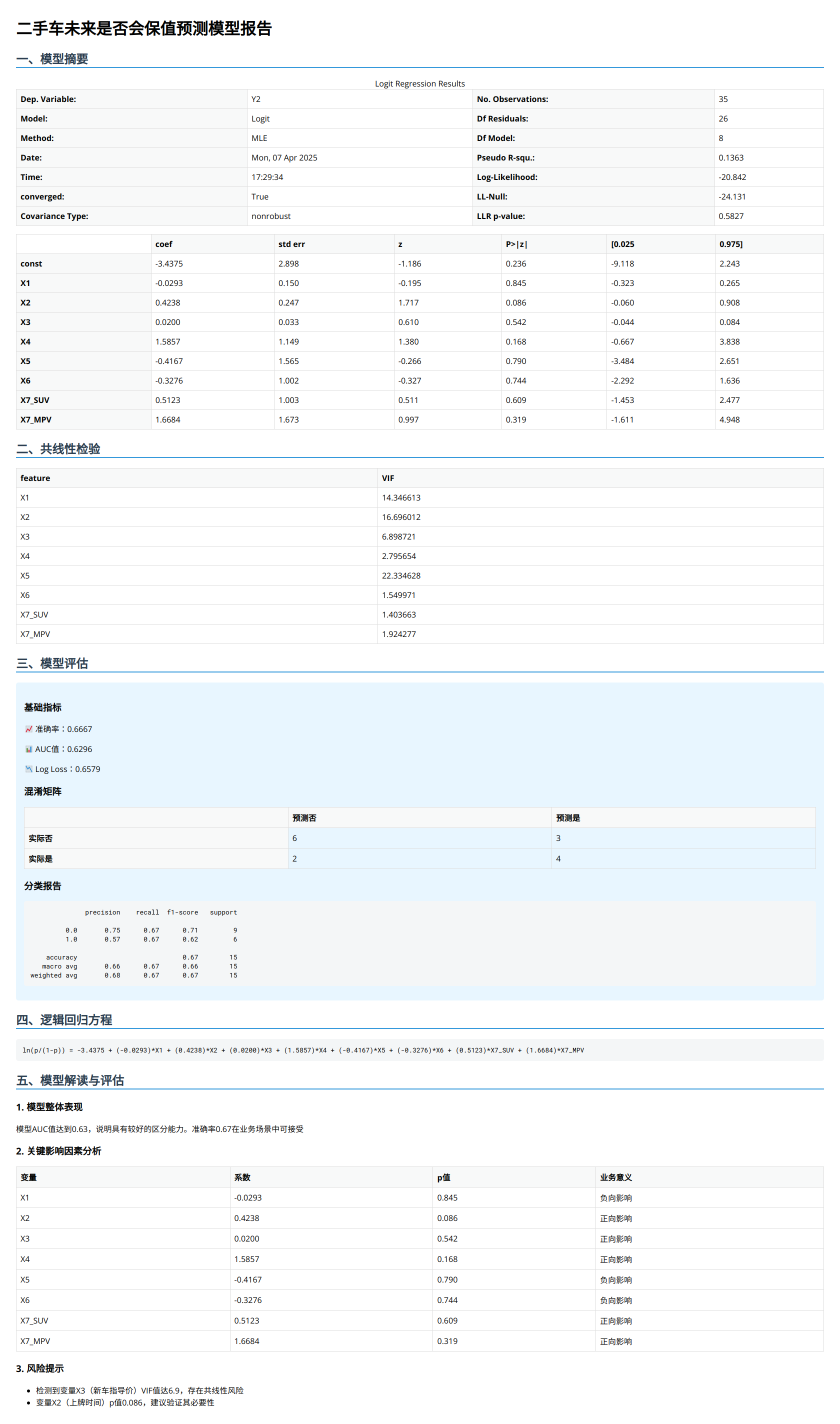
是否保值预测公式Y2= ln(p/(1-p)) = -3.4375 + (-0.0293)*行驶里程(万km) + (0.4238)*上牌距今年间隔 + (0.0200)*新车指导价(万元) + (1.5857)*中控屏 + (-0.4167)*排量 + (-0.3276)*BBA品牌+ (0.5123)*SUV车型+ (1.6684)*MPV车型

假如新上架一辆二手车，对应的变量如下，求Y2

• X1 行驶里程数：12
• X2 距今上牌年份间隔：6
• X3 新车指导价：29.75
• X4 是否有中控屏：1
• X5 排量：2
• X6 是否BBA及以上：0
• X7 SUV车型：0
• X8 MPV车型：0

预测：未来保值的概率为0.52

模型解释

• X2上牌距今年间隔增加1年，其Odds Ratio=e0.4238≈1.528，即距今车龄增加1年保值的的概率增加52.8% ，当然该指标也没有那么显著地影响到是否保值（Odds Ratio= P/(1-P)，优势比），车龄越长反而越保值有点反常识的，但仔细思考，新车转手卖成二手车会大幅贬值，时间越长它的贬值幅度反而变缓。由此，也说明该变量更做时间衰减处理，这里就先不展开了。

以上，利用回归模型进行预测和变量解释。方法比较简单，不管是预测还是变量解释性还有一些调优的空间，在后边的文章中会再详细介绍。

但是，可定量衡量自变量对因变量的影响，对一些因素的重要程度进行判断，已经可以帮助我们在纷繁的因素中，找到方向和重点。