一文读懂AI基础知识:核心流派、算法原理与实战解析
在当今科技飞速发展的时代,人工智能(Artificial Intelligence)作为模拟人类智能的前沿科技,是最具影响力的技术之一,其核心在于通过算法与数据驱动实现感知、学习与决策能力。人工智能广泛应用于各个领域,是第四次工业革命的核心技术驱动力。本文将深入浅出地介绍 AI 的基础知识,包括流派、算法思想、机器学习的任务类型与工作流程、以及其中涉及的数据和数学知识,并以鸢尾花分类为案例,拆解机器学习过程,帮助大家了解理论与实践相结合的知识体系。

一、人工智能流派
人工智能(Artificial Intelligence)并不是简单的“投入多少人工,就能产生多少智能”,它是通过算法与数据来实现智能化的决策。人工智能的算法代价很高,它不能解决所有问题,所有的智能都需要通过野蛮的数据计算来置换,从工程应用的角度来说,优先选择简单有效的方式,人工智能是最后的选择。人工智能主要有三大流派:
行为主义人工智能
拥有一套自动控制系统,能感知外界的变化,并自动做出相应的反馈,比如工业机器人,包括:机械臂、机器人、机器狗、无人机等,还有比较热门的具身智能。
符号主义人工智能
最典型的应用是专家系统,缺点是泛化能力不足,比较依赖知识图谱、大模型+知识库,需人工构建知识库,难以处理模糊的规则及超出知识库之外的情况。
联结主义人工智能
联结主义主张模拟人脑设计,通过模仿人类的大脑,用全连接方式代替机器学习,深度学习就是联结主义人工智能的典型应用,包括用卷积网络用来生成图像视频、循环神经网络和多头(自)注意力机制对应时序数据、基于transformer架构的GPT模型等。特点是泛化能力强,善于处于非线性问题。
融合统一是发展趋势
大模型对 NLP 的整合、多模态对 CV 和 NLP 的整合,以及具身智能(动作+多模态大模型)的发展,都在一定程度上推动着人工智能的加速融合,理论上联结主义用数据驱动学习、符号主义用知识约束推理、行为主义用环境感知迭代,而现实任务往往需要三者结合,人们需要的是具有自主感知、认知、决策、学习、执行以及社会协作能力的通用人工智能体,这种“混合智能”更接近人类的多维度认知方式。
二、人工智能算法思想
在数学当中有函数对应关系:y=f(x),在人工智能领域中黑盒思想是我们理解计算方式的第一法则,给计算机指定一个解决思路,具体的解决过程是计算机去完成。即有输入:x,有转换关系:F(x),有输出:y。
传统算法是基于规则的算法,适用于规则比较清晰的场景,比如在多轮对话任务的智能客服系统,因为规则是人为规定的,所以这类系统对人的业务熟练度要求比较高,但是对计算机的性能要求相对低,特点是执行速度快,算法和时间、空间的复杂度低。
人工智能算法是基于数据的经过训练和推理的算法。训练阶段:从老数据,一般叫训练集中挖掘规律,构建算法规则,然后进行推理,即把规律作用于新数据(测试集),这种经过训练推理的方法适用于规则比较模糊的场景,特点是执行速度慢,对计算机性能的要求很高,需要大量的数据与算力,对算法工程师的要求低,执行效果的鲁棒性特别好,泛化能力极强,但解释性差。
三、机器学习(Machine Learning)的任务类型与学习方式
广义的机器学习主要是一个研究如何让计算机通过数据学习规律,并利用这些规律进行预测和决策的过程。这里的Machine并非物理意义上的机器,可以理解为计算机软硬件组织;Learning可以理解为一个系统或平台经历了某些过程后,性能得到提升,这个过程为学习,是个动态过程。
3.1 机器学习任务类型
分类:将数据样本划分到定义好的类别中,比如鸢尾花根据花瓣和花萼的属性,将它分为3种类别,类别标签可以用0、1、2来表示,通常放在样本数据的最后一列。
回归:根据输入特征来预测一个值,跟分类任务不同,回归任务预测的值通常是连续的值,比如根据房子的城市、地段、大小等预测房价。
聚类:将数据样本划分成不同的组,同一组的样本具有较高的相似性,比如将具有相似消费行为的客户分成一组,以便企业进行精准运营。
3.2 机器学习的学习方式
人工智能要按照训练数据有无标签可分为有监督学习、无监督学习和自监督学习
有监督学习:有特征、有标签,在分类问题中,标签是在有限的类别中选择一个,比如:性别、左右、对错等,在鸢尾花分类任务中,共几百个样本,4个特征,3个类别;回归问题的标签为连续变量,通常用来预测一个值:比如:身高、年龄、股价等。
无监督学习:有特征、无标签,即通过模型自主从数据中提取信息,比如降维算法、聚类算法,通过无监督学习可以将高维数据降维,去除冗余信息,降低计算成本。
自监督学习:base大模型的训练进行学习,让模型自动从数据中挖掘出有价值的特征,比如利用大量无标签数据进行预训练,学习到通用的特征表示后再进行进行微调,提升模型的性能。
四、机器学习的工作流程
如果决定要用人工智能去解决一个问题,具体的步骤为:
1.分析问题
从宏观角度分析问题,确定输入和输出以及任务类型,比如做一个中英翻译器,输入中文,输出英文;房价预测输入房子特征信息,输出价格;人脸检测输入图片,输出检测到的人脸。
2. 采集数据
根据输入和输出构建数据集,在机器学习领域,数据集通常以二维表格形式呈现,一行一个样本,一列一个特征,最后一列是标签或回归数值。按照训练数据的特点,可选择对数据进行预处理,常见的机器学习数据预处理方法有:
- 中心化:数据范围较大、偏移某个基准明显,减去均值使数据范围围绕0点波动,这样可以减少数据的偏移影响,让模型更容易学习数据的规律。
- 标准化:特征尺度、量纲不同、且算法关注分布规律时,将数据减均值再除以标准差,缩放到均值为0、标准差1的正态分布,确保不同特征在模型训练中具有相同的重要性。
- 归一化:不同数据取值范围悬殊,例如,一个特征的取值范围在 0 到 1000 之间,而另一个特征的取值范围在 0 到 1 之间,将每个样本数据减去样本最小值再除以样本的最大值减去最小值,会将数据压缩到[0,1]之间,使得不同特征在模型训练中具有相同的权重,有助于提高模型的收敛速度和稳定性。
3. 模型选择与训练
根据任务和数据特点遴选一种合适的算法,将处理好的数据给算法去学习,完成模型的训练,挖掘出输入与输出之间具体的映射关系。常见的分类算法有KNN:K值邻近算法、GNB:高斯贝叶斯算法、DT:决策树算法、SVM:支持向量机算法、RF:随机森林算法、EL:集成学习算法等,在实际案例中需要遵循引入模型、构建模型、训练模型的过程。
4. 模型评估
对训练的模型进行验证和调参工作,通过各种评估指标来衡量模型的效果,如准确率、召回率、F1 值等,找到预测效果最理想的模型参数。
5. 上线部署
工程部署、系统集成,进行本地化部署、云端部署或者边缘部署,云端部署适合数据量较大、计算资源需求高的场景;边缘部署更注重实时性和数据隐私,适用于对响应速度要求高的场景,如政务系统、智能安防监控等。
6. 模型推理
把规则作用于新的数据进行预测,并依据新的数据不断迭代升级。
机器学习的经典案例:鸢尾花分类任务
1. 分析问题,确定输入和输出
在人工智能算法中,所有的实体都需要变成数字才能被计算和预测,如何将一个实体数字化呢?一般用这个实体的特征或者属性来描述,比如:颜色、大小、重量等,这就需要对业务有足够的了解,比如鸢尾花的四个属性(特征):花瓣长、花瓣宽、花萼长、花萼宽,最后一列为类别编号。
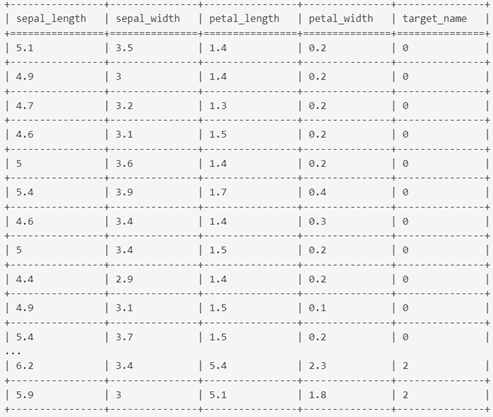
2. 数据采集与预处理
比如每个类别各采集50朵花,按照一行一个样本,一列一个特征组成特征矩阵。对样本进行切割,分为训练集、测试集和验证集,通常会按照60:20:20 或者70:15:15的比例来划分。本次案例分为训练集和测试集,测试集占20%,并确保每次切分的数据保持一致。

3. 选择算法
完成输入到输出的映射,我们选择 KNN 算法进行训练。KNN 算法通过计算测试集与训练集每个特征之间的距离,选择距离最近的 K 个样本,再根据这 K 个样本的类别来判断测试样本的类别。
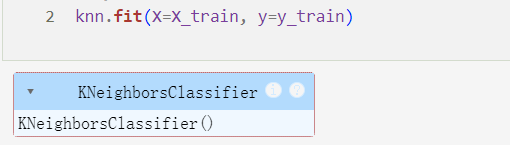
4. 模型评估与部署
用准确率评估鸢尾花分类任务,最终得到的准确率为96.7%,这是一个比较不错的数据,表明 KNN 算法在该任务上表现良好,可以应用到相似场景中,比如在农业邻域中,通过提取植物的特征(如叶片形状、颜色、花朵特征等)对不同品种进行分类。
五、人工智能中的数据和数学知识
5.1 python数据三剑客
人工智能依赖向量化和矩阵化编程,与线性代数密切相关,比如经常用到矩阵乘法,计算过程需要高性能的计算资源,在数据科学中按照维度定义和处理数据。python为人工智能提供了丰富的库和工具,最常用的库有:
- Numpy:进行科学计算,向量化、矩阵化计算,ndarray是 NumPy 库的核心数据结构,是一个具有相同数据类型(如整数、浮点数等)和固定大小的多维容器,容器中每个元素都有相同的数据类型,并且在内存中是连续存储的。例如,一维的ndarray就像一个列表,二维的ndarray类似矩阵,而更高维度的ndarray可以表示更复杂的数据结构,在ndarray结构中,标量(scalar)、矢量(vector)、矩阵(matrix)和张量(tensor),分别表示0维、1维、二维和三维以上的数据。
- Matplotlib:对数据可视化,用一行代码就能实现绘图,直观理解数据的分布和特征。
- Pandas:二维数据分析神器,提供了高效的数据结构和数据处理函数,方便对二维数据的读取、清洗、转换等操作。
深度学习常用的框架有pytorch、tensorflow,pytorch可在官网下载,支持安装gpu和cpu版本。
5.2 数学知识
矩阵
人工智能中处理的大量数据通常以矩阵形式存储和表示,机器学习中对矩阵的处理包括:
- 矩阵分解:用于抽取信息,比如矩阵的特征向量和特征值。
- 特征分解:进行特征分解的矩阵必须是方阵,奇异值分解可以适用于任何矩阵,在PCA降维算法中,能帮助提取数据的主要特征,降低数据的维度,从而提高算法的效率和性能。假设有三个矩阵,分别为A:[m, k],B:[k, n],C:[m, n],则AB=C。
样本相似度度量
1)欧氏距离
建立个直角坐标系,把每个样本看作一个点,有多少特征就有多少维度的欧氏空间,欧氏距离是欧氏空间中用于衡量两个点之间距离的一种度量方式,比如在聚类算法中衡量数据点之间的相似性;在鸢尾花分类任务中,遍历计算测试集与训练集中各个样本的欧氏距离,找出与测试集样本最接近的K个点,距离越小越相似。
在二维平面上,设两个点α(x1, x2)、β(x3, x4),
则α和β两点之间的欧氏距离为:
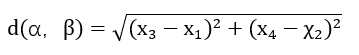
2)点乘积和余弦相似度
每个样本可以看作一个向量空间内的向量,样本的相似度度量方法可以用余弦相似度和点乘积来计算
向量的模(长度):
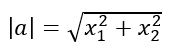
点乘积:
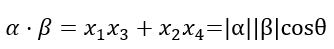
点乘积的值不仅与向量的模(长度)有关,还和向量的方向相关,当两向量夹角为0时,点乘积值最大,两个向量越相似,反之亦然。
余弦相似度:
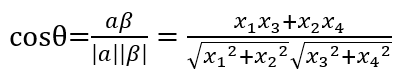
余弦取值范围在[−1,1]之间,值越接近 1 表示两个向量的方向越趋同,则样本越相似;值越接近 -1 表示两个向量方向相反;值接近 0 表示两个向量近乎正交,即样本差异较大。
正太分布
在现实世界中,许多数据都近似服从正态分布,在机器学习中,我们把每个特征数据看作相互独立,通常也假设数据服从正态分布,均值和方差是描述正态分布的关键参数,在计算时可以简化模型计算的复杂度。除此之外,在数据预处理时,对于数据的中心化、标准化和归一化处理也需要均值和标准差。
均值:均值是一组数据的算术平均数,反映了特征数据的中心位置,对于一组数据x1, x2,…xn,其均值为:
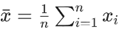
方差:方差用来衡量一组数据的离散程度,方差越大,数据分布越分散;方差越小,数据分布越集中。对于一组数据x1, x2,…xn,其方差为:
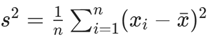
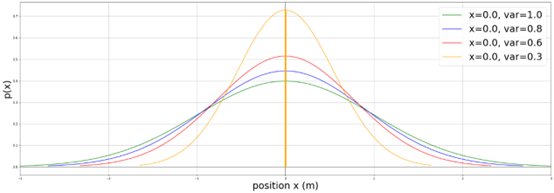
上图显示均值都为0时,拥有不同方差数据的分布特点,其中x代表均值,var代表方差
理论上我们需要求出所有数据的准确方差值,在实际计算场景中,数据量往往非常大,获取和计算数据成本太高,需用样本方差代替总体方差去计算。整体方差是在所有数据参与的前提下计算出的值,样本方差是从总体中抽取一部分数据作为样本。
标准差:标准差是方差的平方根,与方差的作用类似也是用于衡量数据的离散程度,正太分布以均值为中心,标准差越大,数据分布越分散,图像越扁平;方差越小,数据分布越集中,图像越窄长。对于一组数据x1, x2,…xn,其标准差为:
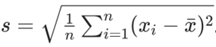
本文由 @AI产品薇薇 原创发布于人人都是产品经理,未经许可,禁止转载。
题图来自 Unsplash,基于CC0协议。
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务。
- 目前还没评论,等你发挥!


 起点课堂会员权益
起点课堂会员权益
 B端产品经理需要更多地进行深入的用户访谈、调研、分析,而C端产品经理需要更多地快速的用户测试、反馈、迭代
B端产品经理需要更多地进行深入的用户访谈、调研、分析,而C端产品经理需要更多地快速的用户测试、反馈、迭代















