每天上下班，习惯了在路上思索人生，而最近半年来一直接触风控算法，所以当我把算法和人生联系在一起时，突然感慨：很多看起来很无趣的算法，居然与很多人生哲理鸡汤彼此呼应。

一、随机梯度算法的“人话”解释

随机梯度算法”与“你要的稳定，不是真的稳定”

1. 梯度的概念

在微积分里面，对多元函数的参数求偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

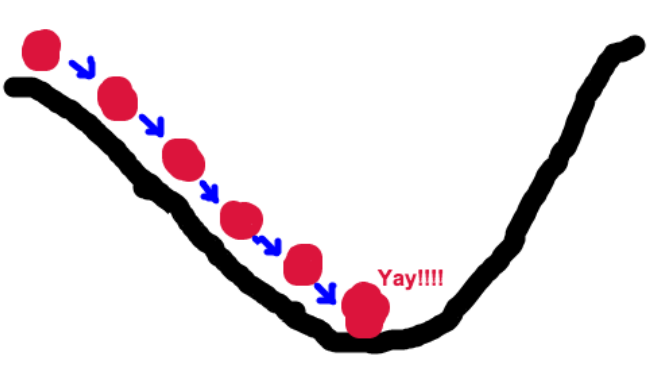
那么这个梯度向量求出来有什么意义呢？他的意义从几何意义上讲，就是函数变化增加最快的地方，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，梯度减少最快，也就是更加容易找到函数的最小值。

如下图所示：

2. 随机梯度的概念

在现实中，我们所遇到的场景是面对的非常复杂、凹凸不平的数据空间，所以想要求解这个函数的最小解是非常复杂的，往往我们会陷入到局部最优的情况中，那这个时候就会涉及到随机梯度的概念。

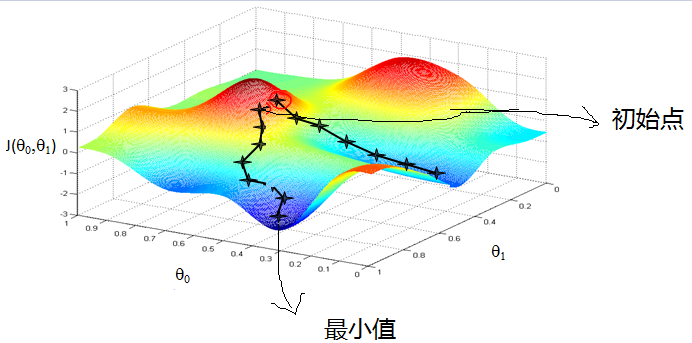
我在这个空间中随机找无数个初始点，每一个初始点都用梯度的思路逐步下探，找到这个初始点的下的局部最优解（最小值），如果我们有足够多的随机值，那么肯定是可以不断逼近整个空间中的最小值的。

如下图所示，不同的初始点按照梯度的想法会得到不同的局部最优解：

3. 随机梯度算法更为通俗的理解

还是不懂？再举一个更加直观的例子，假如你是一只小白兔，从外太空落到地球上来，（地球就是一个凹凸不平的数据空间），对这个星球一无所知，请问如何找到这个星球上的最高点？

那使用梯度的想法就是：小白兔随机在地球上找一个点，然后迈出一小步（梯度算法中的步长），这一步的方向一定是最陡峭的方向（高度提升最快的方向），然后再重复以上的步骤，那么你就可以找到这个点上对应的局部最高点（比如小白兔刚开始选择了黄山市，那么它的局部最高点可能就是黄山莲花峰）。

不断重复上述步骤，在地球上再随机找N多个点，每一个点都找到它对应的局部最高点，你有可能找到泰山、华山等等等等，然后小白兔再比较每一个局部最高点，只要随机点足够多，那它就有可能找到珠穆朗玛峰，就算找不到珠穆朗玛峰它也可能找到高度更接近于珠穆朗玛峰的点（次优点）。

这就是随机的力量！

你要的稳定，不是真的稳定。

如何max（人生自我价值），这也可以看作是一个数据空间中的最优解，实际上也是在人生这个复杂的数据空间内寻找最高点的过程。

每个人可能会选择从事科研、教师、商人等职业，这都是一个复杂的数据空间，选择好初始点之后你就要在这个初始点上不断的去攀登，努力的做好科研、当好一个老师等等，你在这个职业上的每一点进步都是梯度提升的过程。

但是受限于每个人能力、天赋及外部环境的影响，梯度提升的局部最优点是不一样的，有可能到一定阶段之后你就陷入了局部最优的情况，这就是所谓的“稳定”，当然也会有很多人喜欢这种稳定，但是显而易见的，就很难得到max（人生价值）的目标。

我们在选择人生道路的时候，很多时候是基于我们既有的认知去选择初始点，对未知的初始点拒绝选择，这就相当于小白兔在视野范围内去找自己能够达到的最高点。

而为了能够实现max（人生自我价值）的目标，就需要打破这种人生的稳定（局部最优），尽量的多去折腾（随机选择初始点），这样的话才更有可能在财富、地位等方面比之前更高（找到比上一次更优的局部最优点）。

其实对于一个企业来说也是这样，一个传统企业和一个创新型企业最大的区别在于敢不敢折腾，传统企业来说可能会把一个业务做到极致了，达到这个范围内的局部最优点了，但是如果一直安安稳稳守本分，这个局部最优点迟早会被其他敢于折腾的公司超越掉，过去二十年见证了多少这样的例子。

当然，如果小白兔运气比较好，初始点就在珠穆朗玛峰山脚下或者山腰上（好的家庭背景或者非常成功的创业方向），它就不需要这么折腾去找下一个最高点了。

所以，那些所谓稳定的人生，无外乎是某一个初始点的局部最优状态，而我们对其他初始点的未知，直接限制了我们可能达到更优点的可能，当然也有可能是个更差的点，但是对于未知的恐惧不应该成为我们打破稳定状态的借口，未知才有可能。

在波诡云谲中刻意去维持不变，就好比削足适履、因噎废食，一潭死水又怎能抵住突如其来的阵阵涟漪呢？

二、逻辑回归算法的“人话”解释

“逻辑回归算法”与“成年人的世界没有对错，只有利弊”

逻辑回归算法是目前在二分类领域用的最广泛的算法，大概的展示如下图，而其中的Z是一个简单的多元多项式：Z=a*x1+b*x2+c*x3+…+常数项，x1、x2等就是一个描述性，自变量，如年龄、性别等，而y最终的结果是一个在（0,1）之间的常数。

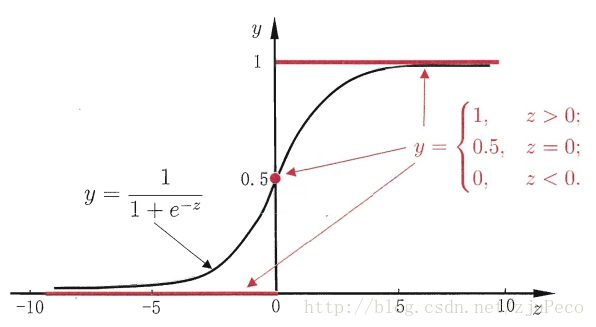
因为逻辑回归算法的稳定性、易解释性，目前已经成为银行信贷风控领域常用的算法，而多项式Z是一个关于年龄、性别、学历、资产等多方面维度的表达式，通过这个算法我们可以计算出一个用户在某一项信贷业务中的违约概率。

一般来说逻辑回归算法最终得到的结果是无限趋近于0或者无限趋近于1，在信贷领域就代表该用户违约概率基本为0，或者该用户最终基本可以确定坏账了，但是这也是一个可能性。

概率这种问题在信贷到期日真正到达之前，违约的可能性就类似于薛定谔的猫，不到最后一刻我们永远不知道该用户最终是否会赖账不还。

另外我们发现当Z无限大的时候，y趋近于1；当Z无限小的时候y趋近于0，这就代表如果Z的多项式中如果某个变量足够大的时候，会让y无限趋近于0或者1的，比如该用户名下房产1000万且没有任何负债，那我们基本可以断定该用户信用卡不会成为坏账的。

但是0.5不一定能够作为我们做出选择的标准，这得看我们对另一个选择的风险接受程度。假设在信贷行业y=0.4的时候用户有20%的概率会逾期，但是这远远高于我们的风险接受程度，所以我们可能只会接受y<0.3时候的选择。

成年人的世界里没有对错，只有利弊与原则。

在小时候，我们回答某个问题最终都会以正确与否来判断，但是随着我们逐渐迈入社会，我们发现自己面对的问题已经不是一个简单的对错可以解决的了，因为我们遇到的问题大多数情况下都会是一个复杂的系统性问题，影响对这个问题的判断因素有很多，有正向因素、逆向因素，单纯的对错已经不能够描述我们成年人世界里的问题了。

举个最简单的例子，我们在微博上看到的任何社会热点的帖子，都会有正反面双方的意见，而影响这些意见的因素是多方面的。

正如上面的公式一样，影响一个人是否会还款的因素是多方面的，有的因素是正向的，有的因素是逆向的，我们没办法准确的判断一个人是否会还款，我们只能计算出该用户有多大概率是会还款的。

同样，在我们遇到的问题中因为影响因素的复杂性，所以最终这个问题往左走还是往右走是不确定的，不到最后一刻谁也不能预判事情的走向，而每个人根据自己过去的认知水平、立场等会做出不同的意见也是司空见惯的。

当然，同信贷行业中客户净资产很高逾期概率很低一样，在我们遇到的诸多复杂的系统性问题的时候如果某一项因素影响非常大，往往会产生一边倒（y趋近于1）的结论：

比如在幼儿园门口砍杀数名幼童的恶意犯罪行为，这个行为变量x1前的系数足够大，就足以影响让y基本可以趋近于1（执行重罚的决定），哪怕这个罪犯有很多其他因素，比如x2（心理受过伤害）、x3（被欺负过）等其他原本让人同情的因素，也改变不了y的大小。

但是同样如信贷行业，因为我们的风险接受水平不同，所以有的时候y较大的时候，我们最终仍然会选择相反的结论。

比如韩国有一部电影《熔炉》揭露校园性侵犯的电影，在国内处于禁止放映状态，虽然这部电影很好的反映了社会阴暗的一面，大部分的人都是对该片持支持态度的，但是最终还是选择了禁止放映。

这是因为我们没有办法接受如果选择放映了之后可能会激发校园中潜在犯罪分子的犯罪热情，这样的伤害是这个社会不能接受的。所以即使大多数人选择支持这部电影，但是我们仍然禁止这部电影的原因，因为选择放映之后的风险水平超过了我们的接受水平。

以上这点在道德和法律的平衡上也有一定体现，这一定程度上也支撑了道德和社会舆论不能凌驾于法律之上的共识，最经典的例子就是：一个小伙因为母亲生病没钱无奈去抢劫，是对还是错？

原来那句鸡汤的原话是：成年人的世界没有对错，只有利弊。但是除了利弊之外，其实我们还有很多原则要去坚守的，永远不能违背自己内心，这就是算法中的风险接受水平，也是我们自己的最后底线。

于是在我们踩过足够多坑之后，我们学会在做选择之前会尽可能将所有因素考虑进去（即Z中尽可能包含足够多的影响因素），并坚守自己的原则底线（风险接受水平）。

“成年人的世界里没有对错”，这句话看起来残酷，其实更多的是代表我们这个世界的系统复杂性以及理性思考的结果。

“知善知恶是良知，为善去恶是格物”，趋利避害是人的本性，而成人的世界是取舍、因果。我一直在坚持的一句话就是“永远不要让明天的自己成为今天的讨厌的那种人”。

三、随机森林算法的“人话”解释

“随机森林算法”与“兼听则明，偏信则暗”

所谓随机森林，需要理解2个词，一个叫“森林”，一个叫“随机”。

1. 森林

所谓森林，就是有很多棵树组成，这里的树就是我们常见的“决策树”，所以，可以先最简单的了解决策树。

比如希望根据一个人的性别、年龄、身高和收入来判断，是否要考虑跟他相亲，用决策树可以这样去设计算法：

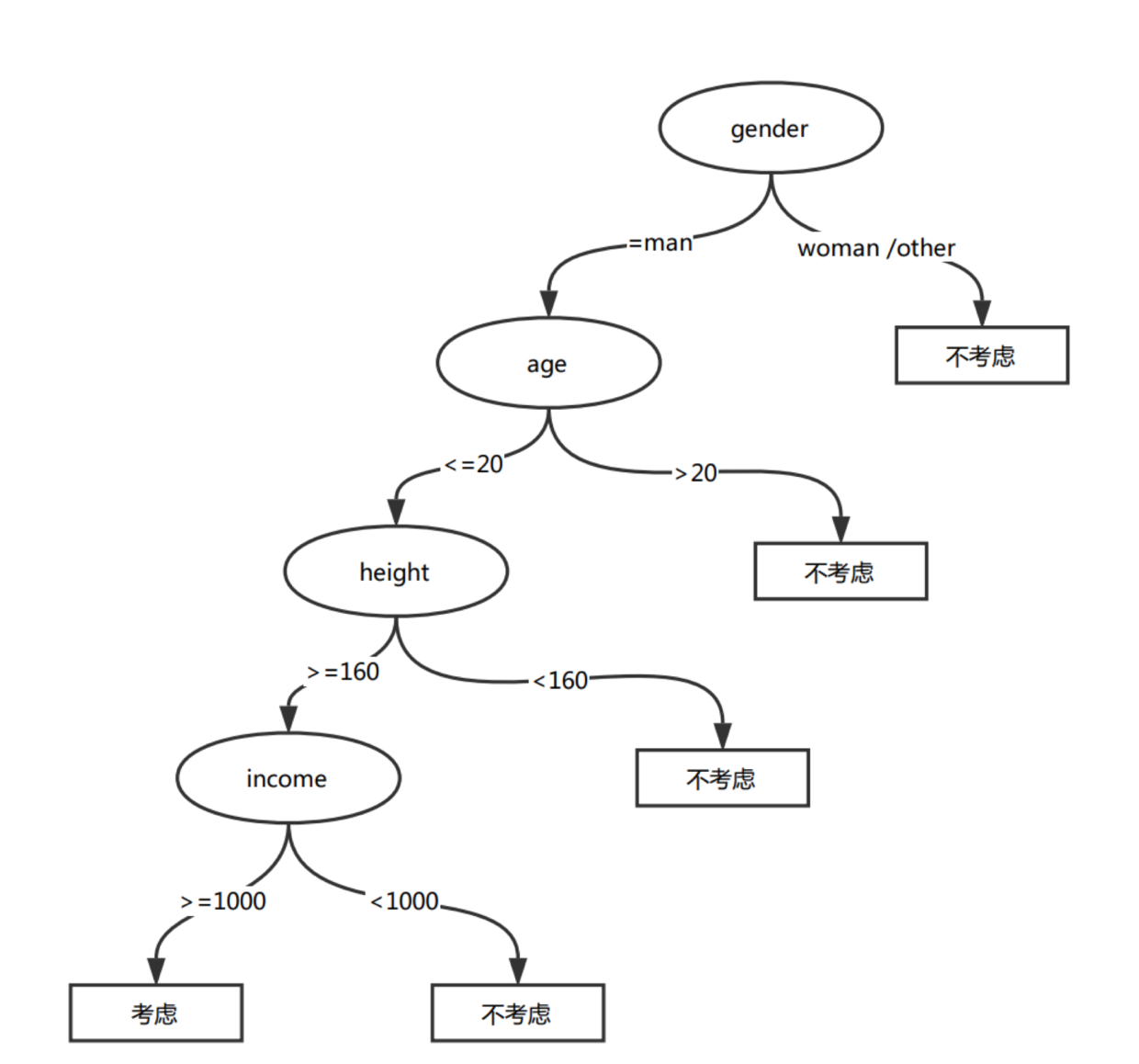
上图是一个非常简单的二分类的决策树，当然在现实运用中数据更多维、更复杂、场景也更多样，所以对于特征选择的顺序、特征分裂点都有非常复杂的处理机制。

当关于一个问题，有很多很多的决策树对这个问题进行表达，这就形成了一个森林。

2. 随机

当影响因素足够多的时候，因素之间存在的相互影响又会很错综复杂，那么一棵决策树的构建过程中受到种种要素影响就很难做出科学决策，那么这个时候就要引入随机森林的生成方法：：

• 从样本集中通过重采样的方式产生n个样本
• 假设样本影响因素有a个，对n个样本选择a中的k个特征，用建立决策树的方式获得最佳分割点
• 重复m次，产生m棵决策树
• 多数投票机制来进行预测

需要注意的一点是，这里m是指循环的次数，n是指样本的数目，n个样本构成训练的样本集，而m次循环中又会产生m个这样的样本集。

所以随机森林也可以称做“民主集中制在决策树上的体现”。现实中当一大群人对某一件事情做集体决策时，每个人本身就是一棵决策树，每个人基于自身利益、对于该事件的不完全信息，于是会产生不同的决策，当有很多人参与投票，人与人之间是随机的不相关的，那这个结果就是随机森林的过程。

兼听则明，偏信则暗。

在现实生活中，我们会遇到可能需要咨询身边朋友建议的复杂问题，比如这套房该不该买、他的求爱该不该接受，但是还有一句话叫“如人饮水冷暖自知”，你向你的朋友咨询的问题往往会得到相悖的结论，因为每个人给你的决策都是基于他的认知、他的利益考量、他的价值观等。

以上文相亲决策树为例，一个好的朋友的建议（一个好的决策树）的前提是这个朋友一定要比你还要了解你的情况、对方的情况以及站在你的利益最大化的角度去抉择，当然这种情况基本不太可能。

如果你只问一个女性朋友并且只采纳一个女性朋友的建议：如果该朋友是一个“塑料姐妹花”，她嫉妒你找了一个非常优秀的相亲对象；亦或她有过一段失败的相亲经历；又或者她的角度问题（如她已经30岁了，男方35岁，而你只有22岁）等因素，基于她片面的认知产生的这棵决策树结论对你来说是不合适的，这也是决策树不可避免的一个问题“欠拟合”。

那这个时候最有效的方法就是尽可能去问更多的人（更多的决策树），每个人会基于自己的理解做出一个判断，这些人要足够多、足够随机、每个人了解到的信息可以互补，那么理论上最后你就可以得到一个最适合你的决策。

当然随机森林的条件在现实中不可能完全满足，DO/DON’T虽然是一个简单的选择但是背后是有非常复杂的逻辑的，所以为了践行随机森林算法的思想，考虑不同群体、不同立场、不同分层的意见，在此基础上做的决策哪怕做不到最优那么也是能够尽可能达到次优的。老祖宗们“兼听则明，偏信则暗”的观点也是带着“随机森林”的思想的。

 四、结束语

数学是一门逻辑性很严谨的学科，于是乎算法就显得冷冰冰，但是算法的背后更是对问题的系统性思考，这一点跟人生很多道理很类似。

于是，算法和鸡汤，产生了某种联系，冷冰冰的算法背后透着很多温暖的鸡汤，再进一步来看，这些机器学习算法的本质是对复杂的系统性问题的理解，背后透着的更多是对人性的考量，总有一天这些算法也会变得很有温度。

如需了解更多内容，请关注我们，欢迎大家共同交流~

作者：独孤qiu败，微信公众号：互联网风控那些事儿（anti_fraud_share），互联网行业风控产品经理，定期分享互联网风控相关业界动态、系统设计方案、模型算法

本文由 @独孤qiu败 原创发布于人人都是产品经理。未经许可，禁止转载。

题图来自 Pexels ，基于 CC0 协议