基于数据的基准对比，就是通过不断的对比去发现我们的产品距离目标是否达到了？还是有一定的距离呢？

数据的价值需要靠有两点来实现：

• 第一，大数据是需要由小数据的精准、完整、及时；这关系到的是实际业务场景的分析和数据指标体系的搭建，这方面我在后面的文章中会讲解说明；
• 第二，就是数据的比较，只有通过数据的比较，数据才会赋予生命力；一个同比，另外一个是和同行比；如果用更加可执行的语言来说的话，一个是基于基准的比较，第二个是基于不同产品的比较。

上节中我有提过数据分析都是基于一定的目的，基于基准的比较目的是检验我们的产品数据是否达到了目标；基于不同产品的比较，目的是为了测试我们哪一版本的产品设计更加符合用户的需求，这个我们将在下一节中阐述。

基于基准的比较分析——我的的产品达到目标没

从上面的两个描述分析说起，“描述一”中该数据就是一个很简单的陈述，我们无法知道老王卖了1000元水果，这个值是多还是少，是增加了还是减少了，所有这个数据的描述是毫无意义的。

“描述二”中，该描述是有对比，昨天是800元这是一个基于历史数据的基准，今天是1000元是在历史数据的基础上有所增长，所以我们可以认为老王今天的营收多余昨天。

关于对于基准的对比总结了从以下的几个维度分析：如何设定基准、确保统一维度、通过样本数量和数据类型来选取计算公式。

以下我们来一一分析：

1. 如何设定基准

一般来说有以下几种方法：

1）基于这个产品任务以往测试所得历史数据

2）基于已发表科学研究或市场研究的发现

3）同负责产品的利益相关者商议标准

无论用什么方法，不要让分析的产生麻痹你设定特定目标；定义目标并不容易，尤其在你即将开始可用性计划时。不要给你设定的第一目标限制，重要的是你要立即建立一些具体的目标，这样你就能测量改进的效果。

如果发现目标不现实或者不合适，你可以修订它们。如果你发现自己需要去做这类修订，试着在获得经验的早期修订，并用产品来进行最初的测量。不要为适应一个不易用的产品去改变合理的目标。

 2. 确保统一维度

测量目标的最客观基础来自前人或者竞品的可用性研究数据，为了最大化普适性，历史数据应该来自相同的条件下、相似的类型参与者完成相同任务的研究。

举个例子：

从上面的例子可以看出，保持统一的维度，变量的对比之间才有意义。如果描述8和描述9 改成：“描述8：老王卖水果，在山东卖，早上卖了1000元。”“描述9：小李卖水果，在山西卖，卖了1500元”。那这个时候我们就很难断定，卖水果的价格差异，是人的能力问题引起的还是地理位置引起的。所以对比分析确保地理纬度一直才有对比性可言。

3. 计算方法

与上节中我们提到的置信区间的计算方法一样，所用的计算方法主要取决于“数据的类型（离散型二进制VS连续型）和样本量大小”。

（1）离散型二进制数据

离散型数据主要用于测量对比任务完成率这样的指标的时候居多。

1）针对小样本的离散型数据

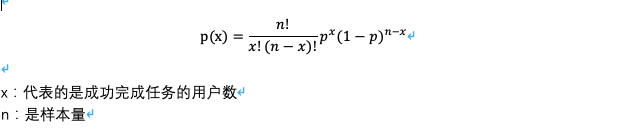
以上公式是“精准概率”的计算方法，还有一个是“中间概率”的计算方法，我们通过以下的一个例子来对比以下，以下两个区间的计算方法有什么异同。

ex：在一场设计初期的测试中，9名用户中有8名成功的完成了任务。是否有充足的证据表明，至少有70%的用户可以成功完成任务？

解：完成率的观测值为8/9=88.9%。假定总体完成率为70%，用二项式精准区间概率可以得到9次尝试中成功8次成功以上的概率。为此，我们计算恰好8次成功的概率和恰好9次成功的概率。

精准概率的计算：9次尝试中有八次成功或者九次成功的概率为0.1556+0.04035=0.1960。换句话说，完成率有80.4%的可能性会超过70%

中间概率的计算：我们使用1/2（0.1556）=0.07782，而不是0.1556。然后把这一半的概率加上9次成功的概率（0.07782+0.04035），得到中间概率值（mid-p-value）=0.1182。现在我们可以说完成率有88.2%的可能性超过70%。

从计算的数值看，“精准概率”的计算方法比“中间概率”的计算方法要保守。

2）针对大样本的离散型数据

上面我们介绍小样本的离散型二进制数据的时，是直接计算p值。在计算大样本的离散型数据的时候需要使用 z 分数来生成p值，只有当样本中至少有15个成功样本和15个失败样本的时候才适用。

只有当样本中至少有15个成功样本和15个失败样本的时候才适用，得到的Z值可以使用Excel公式=NORMSDIST（Z）获得标准正态累积分布到Z的概率值。

（2）连续型数据

离散型数据主要用于在测量满意度评分和任务时间这样的指标居多。

1）评分类数据与基准的对比

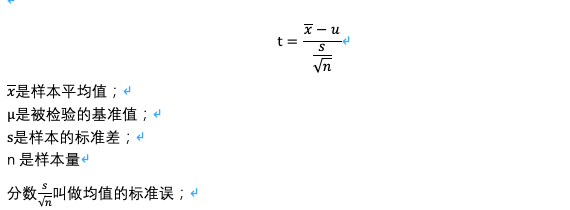
等式告诉我们等式的结果想要告诉我们样本平均值和基准之间的标准差是多少，标准差越大就越说明样本超出基准。在Excel中统计显著性p-value=TDIST（ABS（t）,自由度，方向）；t 需要取绝对值，因为有时候平均值比基准小的情况。自由度=样本量n-1;方向双向检测为1，单侧检验为0。

2）时间类数据和基准对比

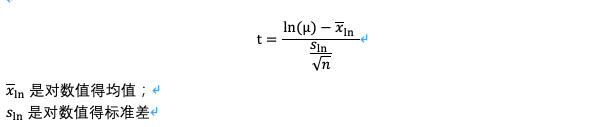
任务时间趋于偏正态（有右侧长尾），大多数统计出来程序基于这样的一个假设：数据近似均匀且正态分布。为了补救这个问题，我们首先将原始数据转化为时间的对数，然后和问卷数据处理方法一样，执行样本t检验。

连续性数据总结：对于连续性数据是根据计算t 值再来转化成p-value值，来对比统计的显著性。同样我们需要计算数值置信区间，看看基准是否落在该置信区间里面，再来判断该对比是否有意义。

总结

基于数据的基准对比，就是通过不断的对比去发现我们的产品距离目标是否达到了？还是有一定的距离呢？以便于发现问题，制定下一步的产品策略。

本文由 @平遥抒雪 原创发布于人人都是产品经理。未经许可，禁止转载