在“A/B测试”和“竞品分析”中，我们如何判断两个版本的产品设计的差别？

上节《数据的比较分析（一）：我们达到或者超过目标了吗？》我们讲述的是产品改版基于目标指标，我们距离还有多远，从而制定改进的产品迭代的策略。

而这节讲到不同版本之间的差异，主要用在“A/B测试”和“竞品分析”中，我们需要判断两个版本的产品设计的差别，如转化率、任务时长、排名；仅仅通过描述性的统计并宣称一个设计的好坏是远远不够的，这时候我们就会发现统计学的必要性。

一、我们从“组内比较”和“组间比较”说起

这里我们常常会涉及到的是“组内比较”和“组间比较”。

组内比较

一般来说是让通一组人参加两个不同版本的设计，这两个版本可能是竞品，可能是一个公司不同产品经理或者UI设计师设计出来的作品；这样的试验好处在于可以排除个体差异对测试结果的混淆。

在这类测试中你需要对用户先接触哪个产品做平衡处理，从而将学习效应的影响降到最低。

如果让用户先体验A产品，无论结果是支持或者否定A产品，都可能存在由于顺序造成的用户偏差风险，这时候组内设计发挥的作用是，将检测结果的差异归因产品间有差异（而非个体的差异），且同样的样本可以检测到更小的差异。

组间设计

组间设计比较的是不同的用户使用不同的产品，不同的用户和不同的设计都会带来变化；所有我们必须检验均值间的差异是否比不同的用户所带来的差异更大。

这里要特别说明一下A/B测试，现在我们常用的AB测试一般来说都是测量的是转化率这个指标，但是转化率这个指标我觉得是一个综合指标，一个转化目标是受很多因素来影响的，例如例如转化目标受产品的可用性、LITT模型等等。

而且在测试期间，为了保证不同版本的测试差异最小，需要的是同一时间、同一场景、同一用户样本，所有这这期间在最短的时间内达到需要的样本容量的话，所受的影响因素会最小。

所以很多AB测试的产品都需要使用的产品在日活达到1000UV以上，这样就能在最短的时间内，达到想要的样本容量。

二、在比较分析时受影响的因素

（1）实验的类型：首先要确定这是组内试验还是组间试验？

（2）样本的大小：其次相对而言是大样本还是小样本？

（3）数量的类型：最后看数据的类型，是连续性数据还是离散型二分式数据？

三、连续型数据的对比

1. 组内比较——配对t检验

关于t值得计算方法：

我们得到检验统计量（t）值之后，为了确实是否差异显著，需要在t表（t-table）中查p 值（p-value）,也可以使用Excel公式=TDIST（）来计算或者核算值。该计算方法无论大小样本都适用。

关于差异的置信区间的计算方法：

配对t检验中的p值只用来告诉我们差异是否显著，但是我们做比较的时候我们还想知道差异究竟有多大既常说的“效应量”；随着样本容量增大（至少100以上），检测结果很容易出现统计显著差异，而实际的效应量却不显著。

差异的置信区间有助于区分细微的（即便是统计显著性的）差异和值得引起使用者注册的差异。

计算差异分数的置信区间如下：

2. 组间比较——双样本t检验

组间比较的时候，不同用户使用不同的产品；不同用户和不同设计都会带来变化。必须建议均值间的差异是否比不同用户所带来的差异更大。

关于t值得计算方法：

这属于双样本t检验，得出的t值需要使用Excel公式=TDIST（t，自由度，样本组数量），通过这个公式来得到p-value值，最后确定两个样本直接是否存在统计的显著性。

关于差异的置信区间的计算方法：

在计算特定水平置信度和自由度下的临界值时的计算方法是：

其中s表示的是分别两个样本的标准差，n表示的是两个样本的样本量;如果手头没有计算工具，且方差又是同质性的时候，你可以通过样本1的数量+样本2的数量-2;如果方差的差异较大（比如两个标准差比例大于2）时，可以采用保守快捷的方法，用较小的样本量减去2。

四、离散型二分式数据的对比

一个二分式离散型变量只有两个值，诸如是/否、已完成/为完成、已转换/未转化

1. 组内比较

连续性的组内检验是(配对t检验)，消除用户之间的差异，所以相比同等样本量的组间设计，组内设计有更高的概率检测到差异。

为了判断两组不同的完成率、转化率或者任何二分变量之间是否存在显著差异，对所有大小的样本我们使用的是McNemar精准检验，通过计算p值来检验异序对样本比例是否大于0.5(也称为符号检验)。

McNemar精准检验：

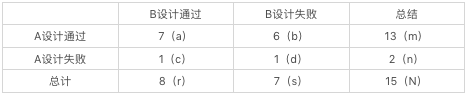
总体来说我们有7对异序对，分布式单元格c和单元格b。

我们将上面表中的数据代入公式中得到：

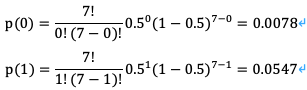
单侧检验的p值是这两个比例的和，0.0078+0.0547=0.0625,因此双侧检验的概率是2倍（0.125）。

若是计算中间概率的话，中间概率等于观测值精准概率的一般，加上小于观测值得所有值得概率和。在上面的例子中，小于观察值的所有值得概率就是零对异序对的概率，为0.0078。

还有McNemar卡方检验，和McNemar卡方检验的耶茨校正；但是不推荐使用，因为对于McNemar卡方检验来说，常常会低估了不同样本容量的真实概率，同时该方法在对样本容量分析效果不明确。而对于McNemar卡方检验的耶茨校正，该方法夸大了所有样本容量的真实值，所有在这里就不一一阐述了。

配对差异的置信区间：

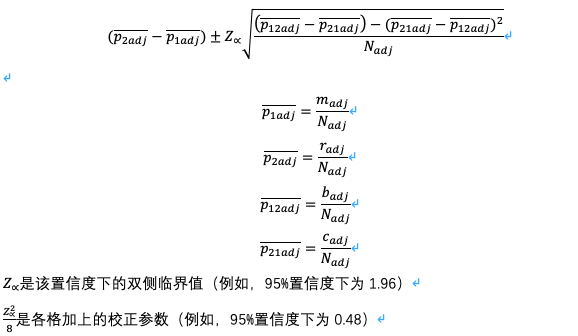
为了估算配对二元结果间可能的差异程度，我们以上公式是采用适当Wald校正置信区间，采用2*2表格进行试验设置，该校正的方法是给每个格子中加上特定置信度下正态分布临界值平方的1/8。在95%置信度下，等于给试验总数N加入了两个伪观值。

2. 组间比较

N-1卡方检验：

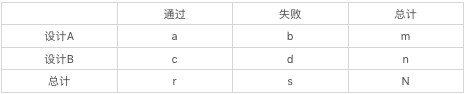
卡方检验计算公式：

在计算出卡方检验的值之后可以用Excel公式CHIDIST（卡方检验的值，1），计算出p-value值；1代表的是双侧检验，0代表的是单侧检验。

N-1卡方检验适用于小样本检验，且期望单元格的次数要大于1使用，N-1是样本的校正值。

N-1双比例检验：

N-1双比率检验样本适用的法则是：每个样本中至少有10个成功，10个失败；且期望单元格的次数要大于1时使用。我们使用一个正态（Z）表查找双侧的p值，或者用Excel公式=（1-NORMSDIST（Z）*2），计算出双侧的p-value值。

N-1卡方检验和N-1双比率检验的对比：

• 计算在数值上是一致的。
• 相比卡方检验用顺利完成或失败的用户量，双比率检验用完成率或转化率（用比例形式测量）的方式思考会更简单。
• 我们采取更加熟悉和容易获取的正态分布作为参考分布计算p值，且无需担心自由度。
• 置信区间公式使用两个比例的差异，在转换中更加容易计算和理解

Fisher精准检验：

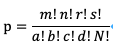
Fisher精准检验使用精准的概率来代替卡方分布和t分布中的估值，精准的计算方法更倾与保守，计算出的p值会比原来的更高一些，因此在两组的差异更大的时候才能达到统计显著。Fisher精准检验是在2*2表中边缘和（m、n、r和s单元格中的值）固定不变的情况下，表内4个实际频数变动时的所有可能组合的概率来计算p值。

适用条件：当有任意一个期望单元格次数小于1时。

配对差异的置信区间：

以下是校正后Wald置信区间，只不过在这里是用于检验两个比例的差异，而不再是一个单独的比例。

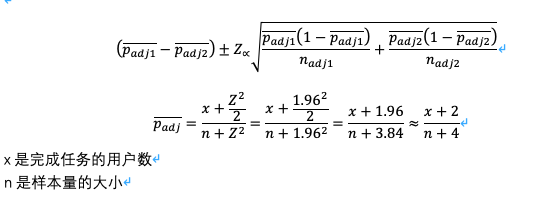
在计算校正计算比例的时候，把分子加上z临界值得平方的四分之一，把分母加上z临界值得平方的二分之一。置信度为95%时，双边检验临界值为1.96。这样做就好比每个样本个增加两个假冒的观测对象——一个成功一个失败

五、总结

上节和这节中我们讲到了很多公式，但是作为一个数据产品经理或者数据分析师，看到数据分析的本质是为了发现问题和解决问题，其他任何方法，都是通往解决问题的一个途径，如何选择最合适的方法解决问题才是关键。

不滞于物，草木竹石均可为剑。

本文由 @平遥抒雪 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议