编辑导语：不论在什么岗位，都要懂得本岗位的基础知识，打牢基础后面才能稳步发展；数据分析也是如此，数据分析必须要掌握统计学的基础知识；本文是作者分享的关于统计学入门基础的知识，我们一起来学习一下吧。

要做好数据分析，除了自身技术硬以及数据思维灵活外，还得学会必备的统计学基础知识！

因此，统计学是数据分析必须掌握的基础知识，即通过搜索、整理、分析、描述数据等手段，以达到推断所测对象的本质，甚至预测对象未来的一门综合性科学。

统计学用到了大量的数学及其它学科的专业知识，其应用范围几乎覆盖了社会科学和自然科学的各个领域，而在数据量极大的互联网领域也不例外；因此扎实的统计学基础是一个优秀的数据人必备的技能。

但是，统计学的知识包括了图形信息化、数据的集中趋势、概率计算、排列组合、连续型概率分布、离散型概率分布、假设检验、相关和回归等知识；对于具体的知识点，本文就不一一介绍了，感兴趣的同学请参考《深入浅出统计学》、《统计学：从数据到结论》等等专业书籍。

统计学分为描述性统计学和推断性统计学。

一、描述性统计

定义：使用特定的数字或图表来体现数据的集中程度和离散程度。

1. 集中趋势

集中趋势集中趋势是指一组数据所趋向的中心数值，用到的指标有：算数均数、几何均数、中位数。

• 算数均数：即为均数，用以反映一组呈对称分布的变量值在数量上的平均水平。
• 几何均数：常用以反映一组经对数转换后呈对称分布的变量值在数量上的平均水平。
• 中位数：适用于偏态分布资料和一端或两端无确切的数值的资料，是第50百分位数。
• 百分位数：为一界值，用以确定医学参考值范围。

2. 离散趋势

离散趋势是反映数据的变异程度，常用指标有极差、四分位间距、方差与标准差、变异系数。

• 极差：为一组数据的最大值和最小值之差，但极差不能反映所有数据的变异大小，且极易受样本含量的影响。常用以描述偏态分布。
• 四分位数间距：它是由第3四分位数与第1四分位数相减得到，常和中位数一起描述偏态分布资料的分布。
• 方差与标准差：反映一组数据的平均离散水平，消除了样本含量的影响，常和均数一起用来描述一组数据中的离散和集中趋势。
• 变异系数：也称作异常值，多用于观察指标单位不同时，可消除因单位不同而不能进行比较的困难。

例如箱线图就可以很好反映其中部分重点统计值：

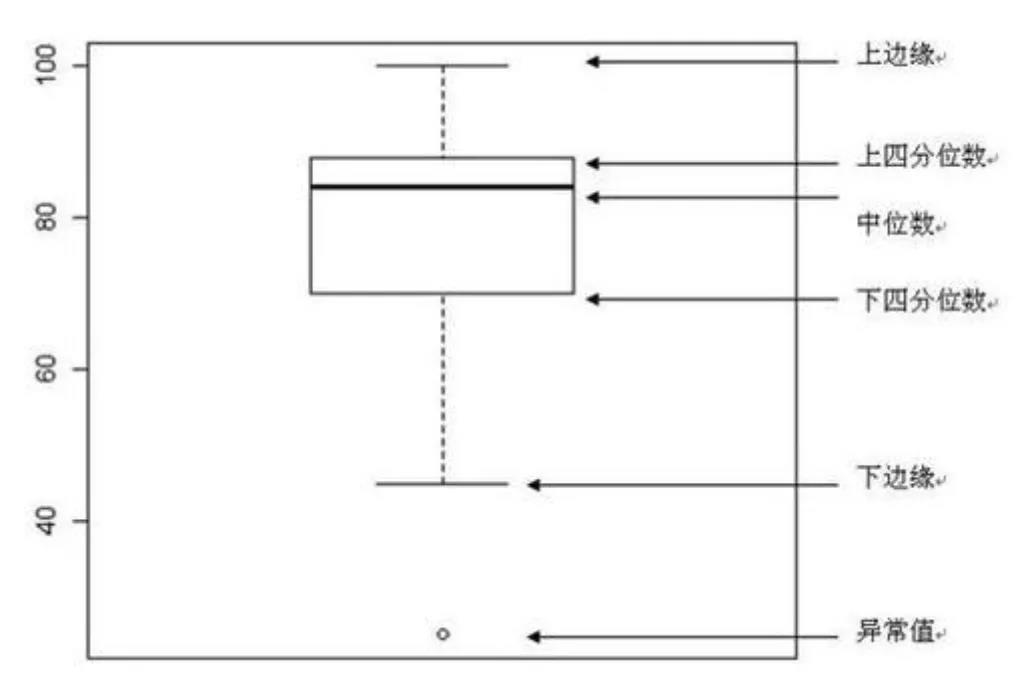
3. 抽样方法和中心极限定理

抽样方法：

我们在做产品检验的时候，不可能把所有的产品都打开检验一遍看是否合格，我们只能从全部的产品中抽取部分样本进行检验，依据样本的质量估算整体的产品质量，这个就是抽样，抽样的定义是为了检验整体从整体中抽离部分样本进行检测，以样本的检测结果进行整体质量的估算的方法。

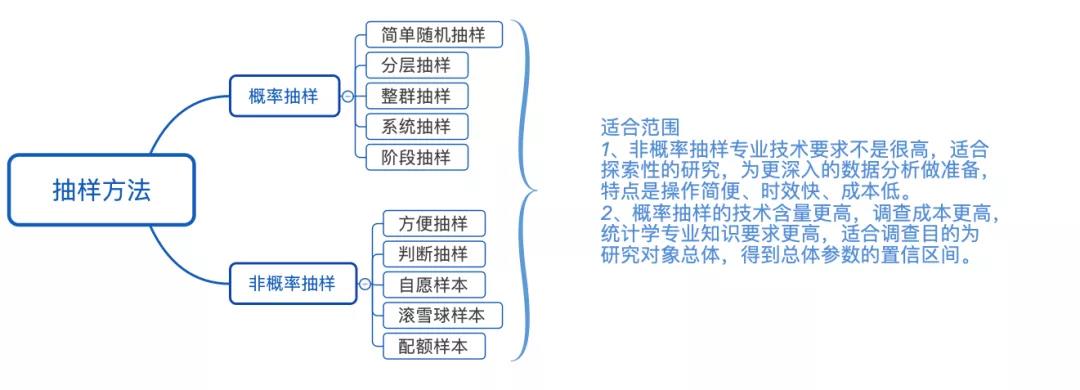
抽样有多种方法，针对不同的目的和场景，需要运用不同的方法进行检测，常见的抽样方法有：

1）概率抽样

• 简单随机抽样；
• 分层抽样；
• 整群抽样（先将总体中若干个单位合并为组，这样的组称为群，再直接对群进行抽样）；
• 系统抽样（将总体中所有单位按一定顺序排列，在规定的范围内随机抽取一个单位作为初始单位，然后再按事先指定好的规则确定其他样本单位）；
• 阶段抽样（先抽群，然后在群内进行二阶段抽样）。

2）非概率抽样

• 方便抽样（依据方便原则自行确定）；
• 判断抽样（依据专业知识进行判断）；
• 自愿样本（调查者自愿参加）；
• 滚雪球样本（类似树结构）；
• 配额样本（类似分层抽样）；

3）两者抽样方法之间的比较：

• 非概率抽样适合探索性的研究，为更深入的数据分析做准备，特点是操作简便、时效快、成本低；而且对于抽样中的统计专业技术要求不是很高；
• 概率抽样的技术含量更高，调查成本更高，统计学专业知识要求更高，适合调查目的为研究对象总体，得到总体参数的置信区间。

4）中心极限定理：

若给定样本量的所有样本来自任意整体，则样本均值的抽样分布近似服从正态分布，且样本量越大，近似性越强。

以30为界限，当样本量大于30的时候符合中心极限定理，样本服从正态分布；当样本量小于30的时候，总体近似正态分布时，此时样本服从t分布。样本的分布形态决定了我们在假设检验中采用什么方法去检验它。

二、推断性统计

定义：根据样本数据推断总体的数据特征。

1. 基本步骤

产品质检的时候用的几乎都是抽样方法的推断性统计，推断性的过程就是一种假设检验，在做推断性统计的时候我们需要明确几点：

• 问题是什么？
• 需要明确的证据是什么？
• 判断标准是什么？

明确后可以对应我们假设检验的几个步骤了：

• 提出原假设（H0）和备选假设（H1），确定显著性水平（原假设为正确时，人们把它拒绝了的概率）；
• 选择检验方法，确定检验统计量；
• 确定P值，作出统计推理；

假设对于某一个器件，国家标准要求：平均值要低于20。

某公司制造出10个器件，相关数值如下：15.6、16.2、22.5、20.5、16.4、19.4、16.6、17.9、12.7、13.9。

运用假设检验判断该公司器件是否符合国家标准：

1）设假设：

• 原假设：器件平均值>=20；
• 备择假设：器件平均值<20；

2）总体为正态分布，方差未知，样本为小样本，因此采用T检验。

3）计算检验统计量：样本平均值17.17，样本标准差2.98，检验统计量为 （17.17-20）/（2.98/√10）=-3.0031

4）当置信度选择97.5%，自由度为9，此时为单尾检验，临界值为2.262。

5）由于-3.0031<-2.262，拒绝原假设，因此接受备择假设，该器件满足国家标准。

2. 假设检验类型

• 单样本检验：检验单个样本的平均值是否等于目标值；
• 相关配对检验：检验相关或配对观测之差的平均值是否等于目标值；
• 独立双样本检验：检验两个独立样本的平均值之差是否等于目标值；

3. 统计检验方法

Z检验：一般用于大样本（即样本容量大于30）平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数>平均数的差异是否显著。

T检验：用于样本含量较小（例如n<30），总体标准差σ未知的正态分布样本。

F检验：F检验又叫方差齐性检验。在两样本t检验中要用到F检验。检验两个样本的方差是否有显著性差异 这是选择何种T检验（等方差双样本检验，异方差双样本检验）的前提条件。

（T检验用来检测数据的准确度，检测系统误差 ；F检验用来检测数据的精密度，检测偶然误差。）

卡方检验：主要用于检验两个或两个以上样本率或构成比之间差别的显著性，也可检验两类事物之间是否存在一定的关系。

4. 双尾检测和单尾检测

这个和我们提出的原假设相关，例如我们检测的原假设：器件平均值>=20。

我们需要拒绝的假设就是器件平均值<20，此时就是单尾检验；如果我们的原假设是器件平均值>20，则我们需要拒绝的假设就是器件平均值<20和器件平均值=20，此时就是双尾检测。

5. 置信区间和置信水平

在统计学中，几乎都是依据样本来推断总体的情况的，但在推断的过程中，我们会遇到各种各样的阻碍和干扰；所以我们推断出的结果不是一个切确的数字，而是在某个合理的区间内，这个范围就是置信区间。

但整体中所有的数据都在这个范围也不现实，我们只需要绝大多数出现在置信区间就可以了，这里的绝大多数就是置信水平的概念，通常情况我们的置信水平是95%。

置信区间[a，b]的计算方法为：（z分数：由置信水平决定，查表得。）

a = 样本均值 – z*标准误差，b = 样本均值 + z*标准误差

志在必得。

不学自知，不问。自晓，古今行事未之有也！

就数据分析而言，我们通过统计学可以用更富有信息驱动力和针对性的方式对数据进行操作；更深入、更细致地观察数据是如何进行精确组织的，并且基于这种组织结构确定数据分析的方法，来获取更多的信息。

作者：木兮&小陌，数据运营；公众号：木木自由

本文由 @木兮擎天＠ 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议