编辑导语：当面临数据存在差异性的情况时，我们需要检验数据差异是由什么原因导致，是否存在真实差异。而假设检验可以通过样本检验总体是否存在显著性差异。本篇文章里，作者结合实际案例，介绍了几种常用的假设检验方法，帮助你检验数据结果是真实差异还是误差。

一、背景

当面临一组数据时，我们很容易发现其中的差异性，比如A方案与B方案的日活用户有差，留存率有差，付费用户数量也有差等等。

但是这些表面上的差异可能仅仅是由这一次抽样误差引起，并不是两者确实存在差异。为此统计学上有针对不同情况下的检验方法，称为假设检验。

本文以抖音为例，简单介绍3种较常用到的假设检验方法：方差分析、独立样本t检验、相关系数的显著性检验以及它们在SPSS中的实现。数据选取抖查查平台显示的截止8月21日抖音粉丝数量前300里去除明星、政务类等达人的数据（存在极端值）进行分析。

二、概念介绍

通过样本检验总体是否存在显著性差异的方法叫假设检验。假设检验中存在两个相互对立、二者择一的假设，一种叫虚无假设H0，另一种叫备择假设H1。

假设检验其实是一种反证法，我们想要得到的结果是A和B两种方案有差异，首先需要假设两者没有差异，通过推翻这种假设来证明两者有差异。

H0就表示两者间的差异仅是抽样误差，H1表示两者间确有差异，通过拒绝H0来证明H1是正确的，就完成了假设检验。根据统计学上的小概率原理，当某事件在一次试验中发生的概率（p）低于5%时，就称此事件为小概率事件，认为它在此次试验中不会发生。此时就可以拒绝H0，接受H1。

下面以3个具体问题为例来介绍上面提到的3种方法。

三、问题一：不同的内容类型是否会影响粉丝数量（使用方差分析）？

在抖音上，不同的创作者基本都有自己特定的内容倾向，一般不会改变，比如有些是生活类，有些是游戏类，那么不同的内容类型会决定粉丝量的上限吗？或者说在头部达人里，是否更高粉丝量的人集中在某些特定领域？

下图显示了不同分类达人的平均粉丝数量（单位：万人）。单看此图，你可能会认为影视娱乐类的内容更容易吸引粉丝，因为此类达人的平均粉丝数量最多，但是这种差异可能仅仅是本次抽样误差导致的结果，为此需要进行的假设检验是方差分析。

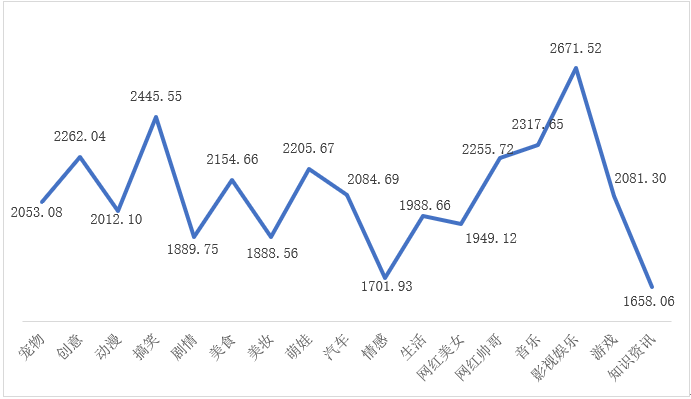
方差分析主要用来检验两组以上平均数的差异问题，在本例中就是检验17个内容类型的平均粉丝量的差异。

自变量为内容类型，因变量为粉丝量，因为只有一个自变量，所以应该进行单因素方差分析。

• H0：各内容类型达人的粉丝量不存在显著差异；
• H1：至少有一组(两个)不同内容类型达人的粉丝数量存在显著性差异。在SPSS中步骤为分析→比较平均值→单因素ANOVA检验。

将粉丝量选入因变量框，内容类型选入因子框，点击右侧选项按钮，勾选方差齐性检验，点击确定。

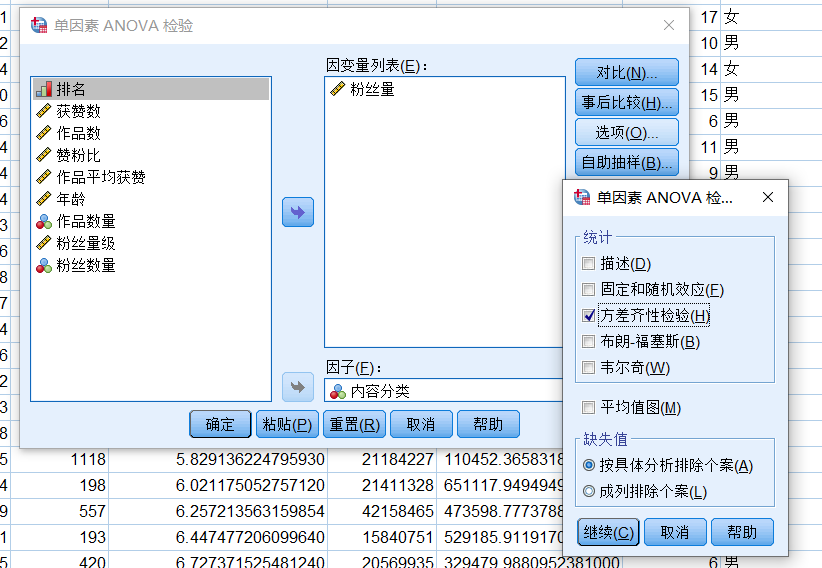
进行方差分析的一个前提就是要保证各组内方差齐性，如果方差不齐则结果无意义。

本例最后的结果显示，方差齐性检验中p=0.528>0.05，各组方差齐性；方差分析中p=0.401>0.05。表明我们不能拒绝H0，即：

创作不同内容的达人粉丝量间的差异仅是抽样误差，每个类型的达人粉丝数量并无显著差异。

（注：假如p<0.05，则还需进行事后检验来检验哪些组间存在显著性差异）

四、问题二：是否签约MCN对头部达人还有影响吗（使用独立样本t检验）？

虽然签约MCN可以帮助一个普通人获得资本的加持，保障内容的持续输出，较快获得流量变现，但是在头部达人中，MCN的作用还大吗？下图显示了两类达人数量及平均粉丝量。能据此作出签约MCN的达人比未签MCN达人的粉丝量更高吗？

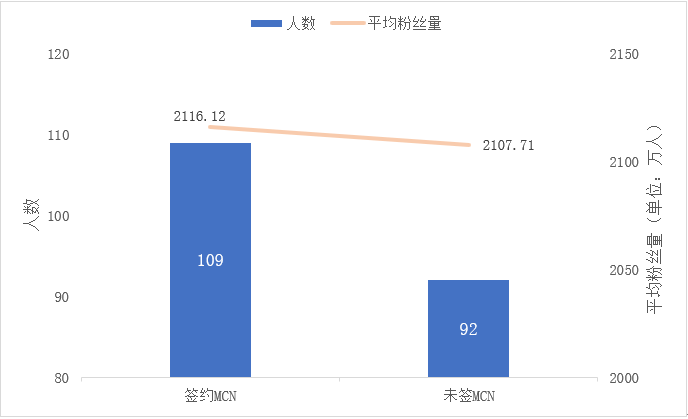
此时需要进行的假设检验是独立样本t检验，它和方差分析的区别在于，独立样本t检验只能处理两组平均数，而方差分析主要用于处理3组及以上数量的平均数。

• H0：签约和未签MCN达人的粉丝量无显著差异；
• H1：签约和未签MCN达人的粉丝量间存在显著性差异。

在SPSS中的操作为分析→比较平均值→独立样本T检验。

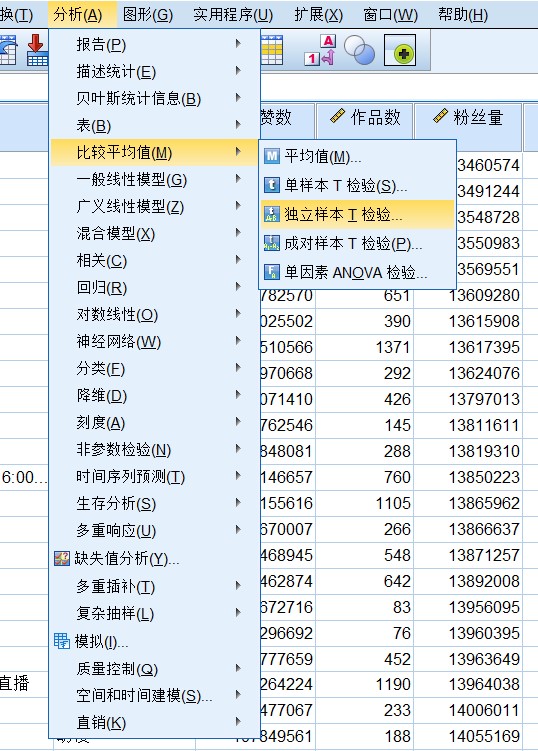
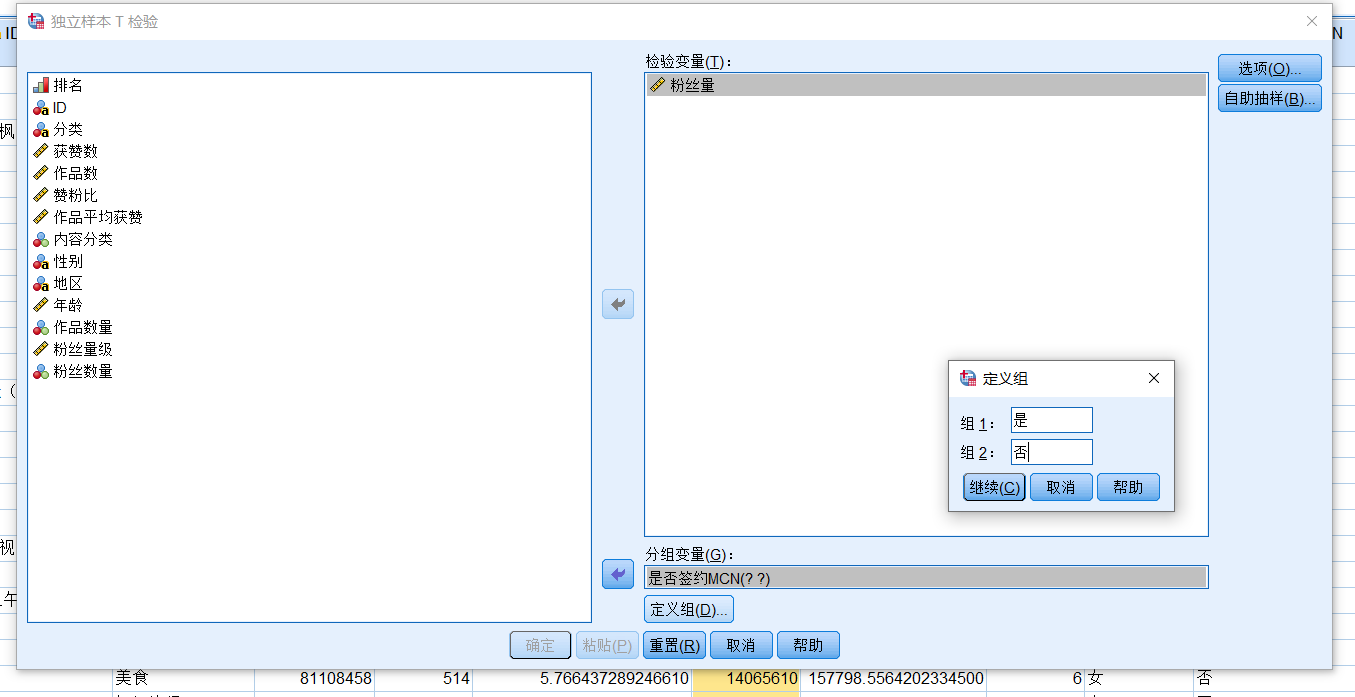
将粉丝量选入检验变量框，是否签约MCN选入分组变量框，点击定义组，组1输入“是”，组2输入“否”，点击继续，点击确定。

结果如下：

在假定等方差时，p>0.05，则不能拒绝等方差的结果，就看此行结果中的t检验结果，p=0.944>0.05。表明不能拒绝H0，即：

在抖音头部达人中，签约和未签MCN的达人的粉丝数量无显著性差异。

五、问题三：以下指标对粉丝数量有影响吗（使用相关系数的显著性检验）？

先来看3张散点图。

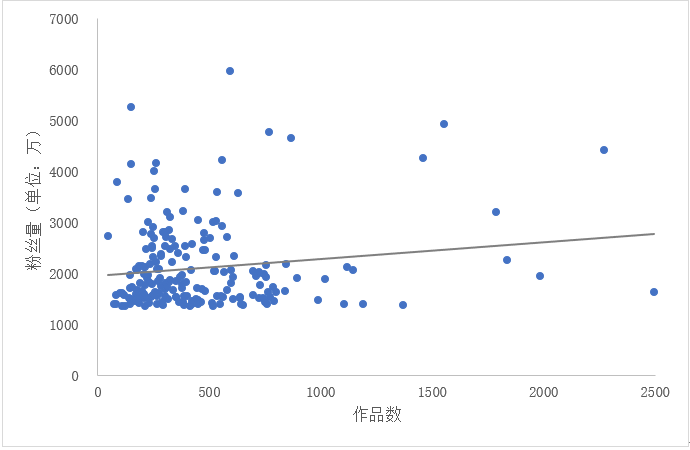
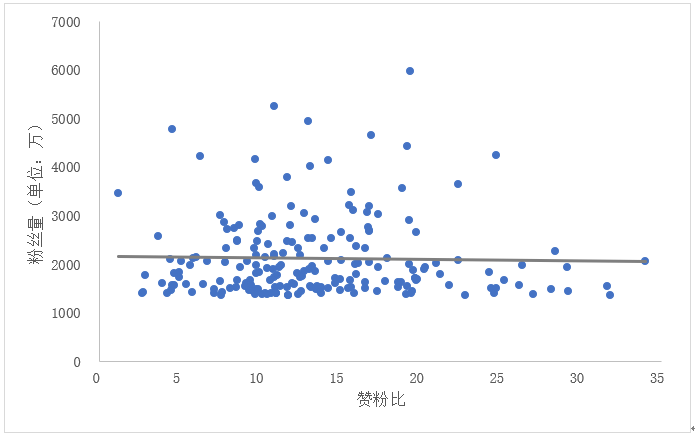
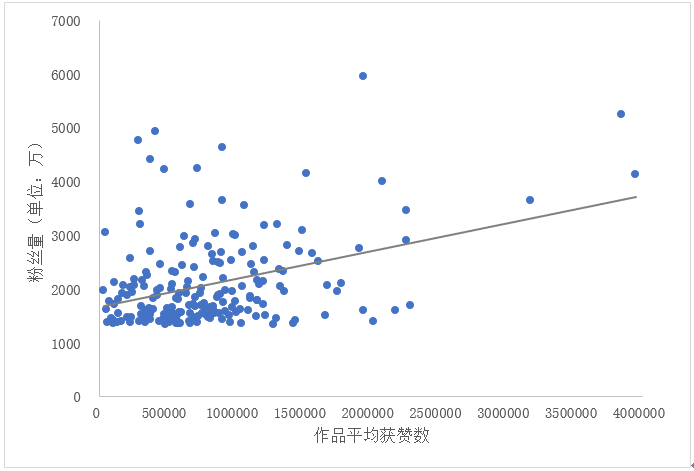
从图中可以看出的是，在与粉丝量的关系上，作品平均获赞数>作品数>赞粉比，检验此结果真实性需要进行的是相关系数的显著性检验，共检验3次。

• H0：粉丝量与XXX的相关系数为0；
• H1：粉丝量与XXX的相关系数不为0。

在SPSS中的操作为分析→相关→双变量。

将粉丝量与XXX选入右边变量框，勾选左下角标记显著性相关性。

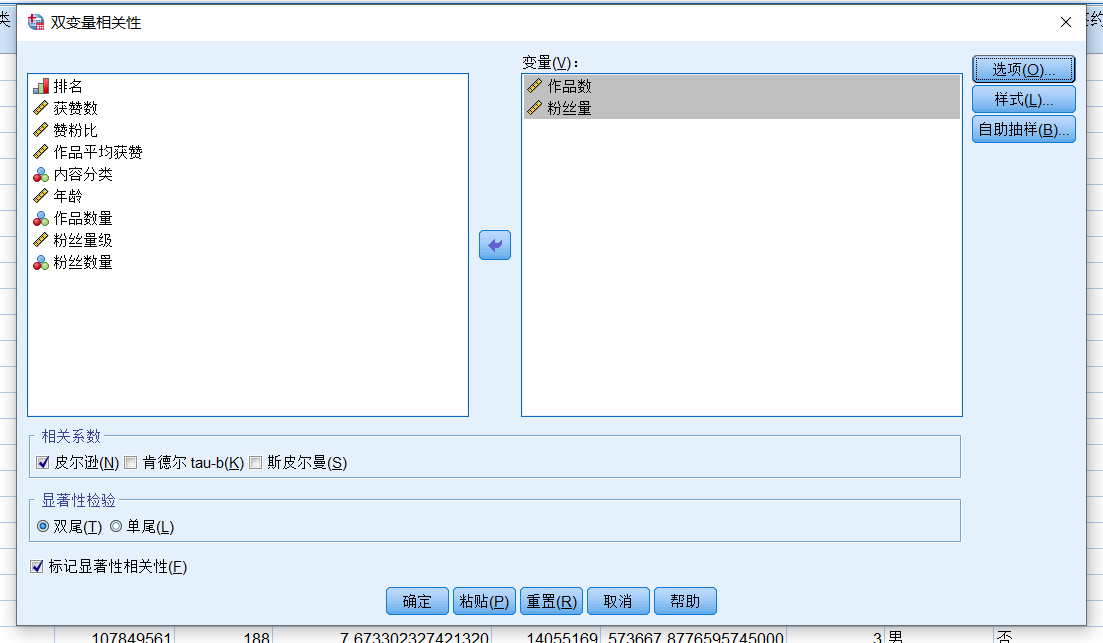
• 作品数的结果显示，r=0.146，p<0.05。说明两者虽然相关，但相关性很弱，即作品数对粉丝量有一定影响，但影响不大。
• 赞粉比的结果显示，r=-0.023，p>0.05。说明二者不存在相关关系，赞粉比对粉丝数量无影响。
• 作品平均获赞数的结果显示，r=0.378，p<0.001。说明二者呈显著的中等程度的正相关，作品平均获赞数对粉丝量影响较大。

检验结果与我们设想的一致，但这并不表示可以直接通过散点图的趋势来判断是否存在显著性相关，相关系数的大小也与是否显著无关，假如相关不显著，那么相关系数再大也是无意义的，需要在相关显著的基础上，再通过相关系数的大小来判断二者的相关程度。

六、结论

独立样本t检验、单因素方差分析和相关系数的显著性检验都是较常用到且基本的假设检验方法，掌握这些方法后可以避免被数据的表象迷惑，对结论做出更准确的判断。关于这三种方法的原理以及更详细的适用条件，读者可以自行查阅统计书籍。

本文由 @flowaa 原创发布于人人都是产品经理，未经许可，禁止转载。

题图来自Unsplash，基于CC0协议。