无关乎算法原理，本文将从用户体验的角度，着重分析多维度数据处理的降维方法：主成分分析法（PC A）

主成分分析法（PC A）：类似SUS，该方法能够将诸多因子如（满意度，可用性，简易性等多指标转化成低维度数据，以数字或图表的形式直观呈现），并介绍反映维度数量与误差性关系的图表–碎石图及其算法（基于PC A）。

前文我们提到了用户体验数据化的广泛例子–系统可用性量表SUS，但是在实际用户体验研究过程中，不光是可用性测量，还涉及易用性，满意度等等其他维度的考量，甚至有些原始数据可能连有哪些维度都是不清晰的，需要研究人员来进行判断。在这种情况下，基于个人经验的判断已经无法适应，我们需要借助计算机与统计学知识来读懂数据以支持产品决策。

笔者并不是理学出身，但基于实际作业的需要，自学了相关课程，感触颇深。如果有线性代数和统计学背景自然是最好的，但是如果不具备，也完全没问题。对于这些方法，如果以产品经理的标准，我们最需要是使用好这些方法，创造价值，所以不用担心。本文将避开算法原理，而重点分析设计逻辑和应用场景。

主成分分析法（PC A）设计逻辑

回顾一下之前的系统可用性量表SUS（详情请看《浅析用户体验数据化》），它本质上是通过投影的方式，将原本两个维度的数据（可用性与易用性）转化在单个轴上。在多维度数据处理中，其核心也是如此也是将：多维度空间的数据通过投影的方式转化在低纬度中。

线性代数告诉我们，如果是单纯的降维，有无数种方式可以进行，难的是在降维过程中，保持原有数据的特征也就是相关性。若两个因子如可用性，易用性是强相关且是线性相关，先假设可用性越高，易用性越高，那么降低维度后，数据集也应当存在这样的特性，甚至能够保持当可用性提高了X%时，易用性也会提高相应的程度。

这里需要注意：数据降维之后一定会损失一定的信息，这没办法避免。PC A做的就是尽量保留主要特征而减弱冗杂信息，所采用的方式是通过让各个原始数据在转化之后，相距尽量大，也就是差异性最明显。

这里先举一个简单例子。比如我们分别给5个产品做了SUS测试得到了每个产品的可用性，易用性指标，我们将其表示在二维图上。

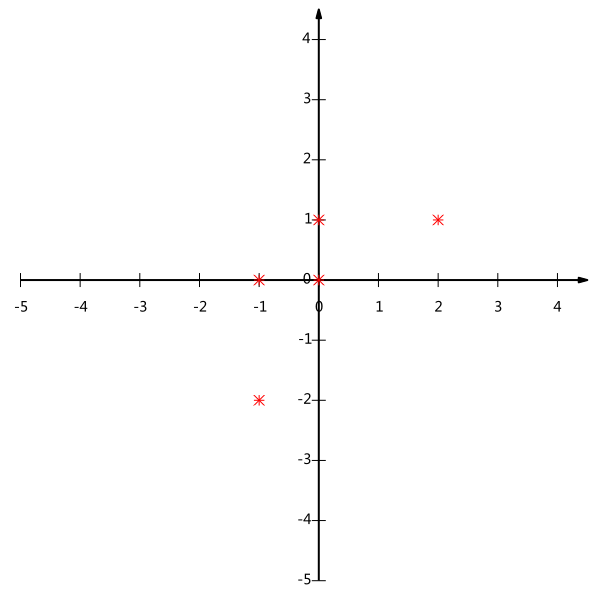
之后我们在将这个两维数据降成一维的。就是找一条轴，然后得到各个产品指标在这个轴上的投影，且满足投影之后的差异性最大。

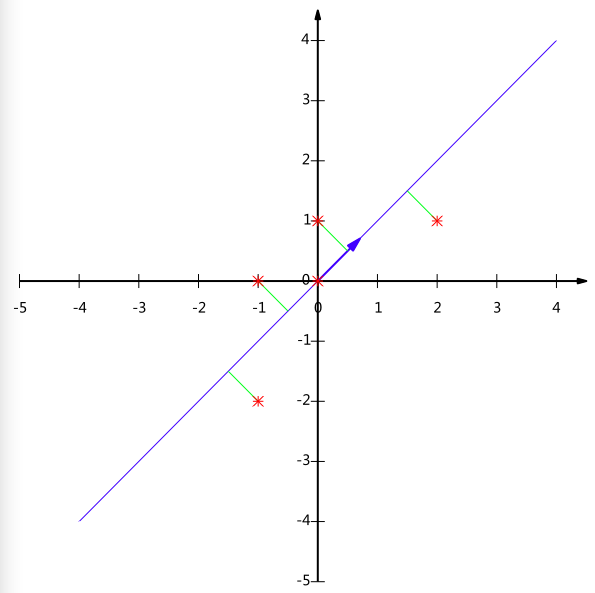
例如产品A（1，2）和产品B（1，0）的关系就保留在了这条轴上。但如果我们投影在了y轴，A和B就重叠了，就无法比较出A和B哪个更优，即丧失了易用性的比较。而PC A算法保留了这个特性，我们通过处理后的数据可以方便的比较各个产品的优劣。

理论上原本有几个维度的数据，就有几个特征向量。各个特征向量之间正交。也就是说明，通过特征向量转换后的维度之间是相互独立的。详细的会在后面的实例中说明。

这里需要特别指出，PC A方法不适合用于高阶相关性的数据，而适合用于线性相关。但对于一般的智能产品领域，或App，网页等互联网产品，社会学研究等，PC A已经能应对绝大部分情况了。

PC A实际案例分析

我将以一个实际的作业来分析PC A的使用方法和注意点。（笔者是用 Matlab 写的程序）。当然，最重要的不是程序而是理解PC A是怎么回事。先附上代码。

%data 为输入的数据集，行表示项目，项目之间是并行的例如产品1，产品2或者用户1，用户2，
%各列表示描述项目的维度比如，易用性，可用性，满意度等
data = shishen;

% PCA Template to data

% n 为测量的项目数量，p则表示描述的维度数量
[n,p] = size(data);

% PC A运算过程，这里就不再介绍，有兴趣可以参考《Exploratory Data Analysis with MATLAB》 。我这里将原数据集其降成一维。

datac = data – repmat(sum(data)/n,n,1);
covm = cov(datac);
[eigvec,eigval] = eig(covm);
eigval = diag(eigval);
eigval = flipud(eigval);
eigvec = eigvec(:,p:-1:1);
pervar = 100*cumsum(eigval)/sum(eigval);
g =zeros(1,p);
for k = 1:p
for i = k:p
g(k) = g(k) + 1/i;
end
end
g = g/p;
propvar = eigval/sum(eigval);
avgeig = mean(eigval);
ind = find(eigval > avgeig);
l=length(ind);

%P 控制转换成几个维度，若需要转换成X维，则p= eigvec(:,1:x);
P = eigvec(:,1:1);
%dataP 即是最后我们得到的降维之后的数据集
dataP = datac*P;

原数据说明

这里我们收集了80位用户在使用某款App时候，在各个任务环节上使用的时间和整体任务失败率，以此得到用户在这款产品上的易用性数值。在以同样的方式进行对竞品的分析，以处理后的数据进行比较，期望得到有哪些环节是关键并且需要改进，产品优势等其他重要结论。

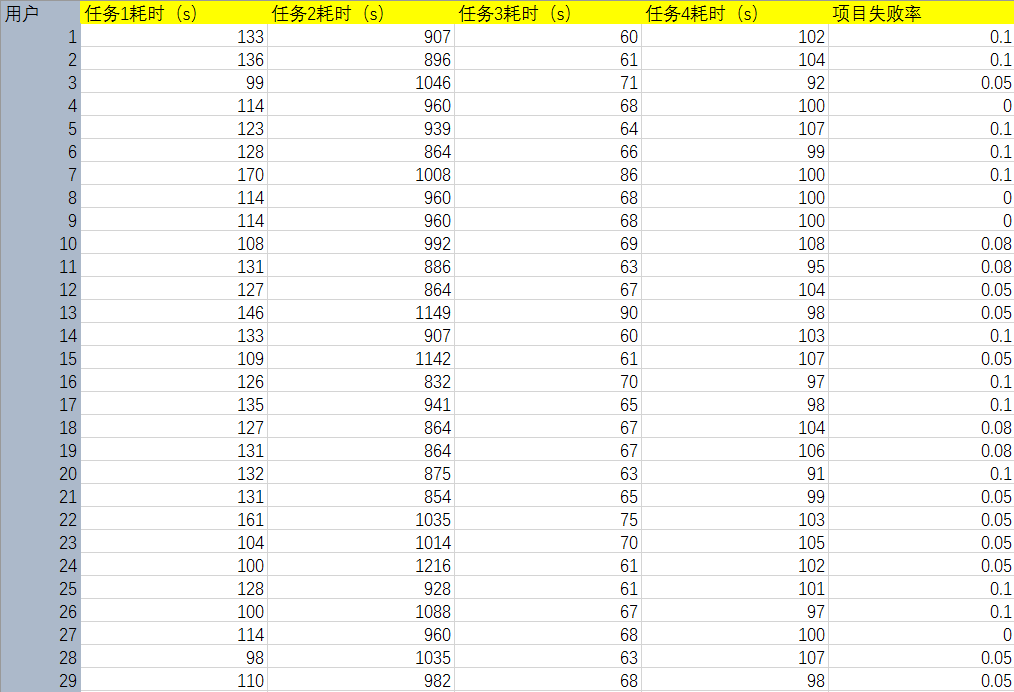
数据需要具有线性相关性

线性相关是保证我们可以找到投影基准的根本，详细的可以参考线性代数等相关知识。我这里指出一个小技巧，在前期数据收集的时候，可以尽量将数据好和坏变化统一。例如上述的例子，我们认为在任务上的耗时越长，表示产品越差。因此使用项目失败率做指标而不是项目成功率，因为失败率越高表示产品越差，而成功率越高表示产品越好和前面的数据变化相反了。通过这样的处理，PC A算法得到的差异性会更加明显。

PC A处理结果及其意义

将以上数据集，用PC A方法降维后，我们得到以下数据集，将这5维的数据转化成只有一个维度，经过与元数据的比较和转换基的数值，我们发现这个分数是易用性维度上的比较。

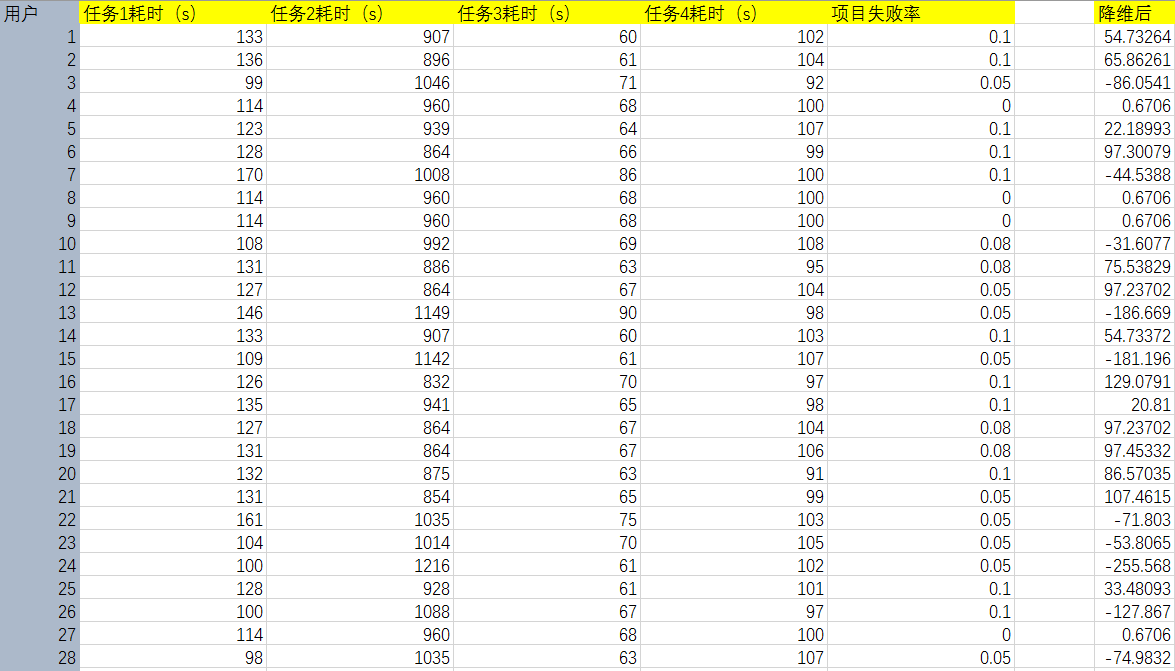
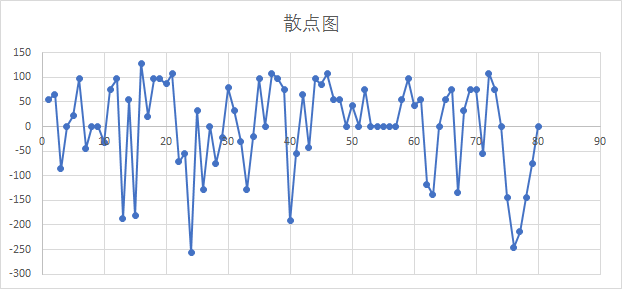
通过分析这个单纯的数据表格，我们至少可以得到以下结论

1. 该App具有一定学习成本，新手导引需要改进，项目分布差值广泛
2. 该App在易用性上存在很大改进空间

在中间过程中，我们得到了以下附属的结果

转化矩阵P

转换矩阵p=[0.0535;-0.9984;-0.015;0.0011;9.9375e-05]。（最大特征向量）。这就是降维转换公式，我们之后再其他产品分析中，用相同的转换矩阵降维就能够像系统可用性量表（SUS）一样进行直观的比较分析了。

那么差值是否具有意义？答案是有意义，这里的差值是可以再次进行运算的。因为转化方程是一致的，所投影的空间也是一致的，可行性单位也是固定的。但是需要注意，经过转换后的数据集是无法再还原到原先的数据集的。因此我们虽然能够比出可行性高低，但是在转换到具体的项目上还需要原来数据的处理。

比如我们在这个项目过程中，通过对最高易用性数值与最低数值原数据集的比较，可以得到各个项目的差异大小。例如得到24号用户达到的易用性数值最高，16号用户易用性最小。然后再原数据中寻找，得到哥哥项目的差是【26，-384，9，-5，0.05】，结合转换矩阵p，我们可以窥视到以下信息：

1. 任务1与任务2在设计上存在冲突，若用户项目A上耗时时间短则在项目B上花费的时间就长。理由是：两者转换值为负相关。
2. 任务2，任务1是关键任务，需要在下一版本中着重设计。项目3，4影响不大，非关键任务，用户犯错率基本稳定。理由是：任务1的1s对应的数值是0.0535的数值变化而任务2中的1s对应的是-0.9984的数值变化。两者对于最后的分数的贡献是不一致的。

数据维度-碎石图

但是以上的转换后的数据有多少可信度呢？理论上，所降维度越低则损失的信息越多。那么如何判断应该降低到几维空间中呢？判断方式就是通过转换矩阵（特征向量）的长度。特征向量长就意味着，在这个维度（例如上述的可用性）上的变化明显，相反，若特征值短就意味着，在这个维度上，数据基本没有差异性因此没有分析价值（大家都一样）。先附上程序。

figure, plot(1:length(eigval),eigval,’ko-‘)
title(‘Scree Plot’)
xlabel(‘Eigenvalue Index – k’)
ylabel(‘Eigenvalue’)

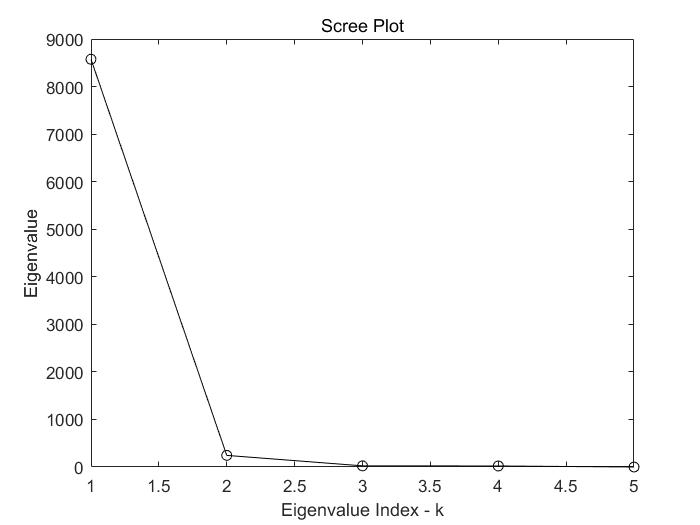
由此看到，这个数据集中只存在一个维度上的变化，这就是主要成分。因此降维之后的信息是具有可信度的，保留了原数据70%~95%的信息。（记住就好）

通过碎石图，我们可以快速的明白数据中有哪些维度需要进行分析。这个k就是碎石图中的拐点，代表了数据需要降低到k维空间中，以保留主要信息。

后记

对于产品经理或者非数据挖掘从业者，了解PC A算法将会使你的分析更加精准有效，使结论更具有说服力，作为初期的用户研究绰绰有余。但本文也只是从用户体验这个侧面展示了这个算法的运用。

通过PC A算法我们可以分析出（不止于此）

1. 项目之间的相关性（冲突还是互利）
2. 项目之间的重要层级和所影响的维度
3. 产品主要维度的构成

这些问题凭借简单的直方图等和肉眼是很难察觉的。因此，毫无疑问，一个掌握数据分析的产品经理所能看到的问题必将更加深刻和现实。

参考文献：

《Exploratory Data Analysis with MATLAB》 Wendy L. Martinez, Angel Martinez, Jeffrey Solka

本文由 @kieran 原创发布于人人都是产品经理。未经许可，禁止转载。