本文主要探寻下信息从输入到锁定再到处理的这个过程中，思维究竟发生了什么，使得它最终形成了框架影响决策。

有这样一个小故事，说是一个集团公司因年度亏损，决定不发奖金，因此老总让三个分厂厂长分别告知员工。

A厂长在大会说：今年亏损，奖金就不发了，会后员工个个大骂厂长。

B厂长在大会说：今年亏损，奖金不发了，而且还得裁人，我力争不裁人，会后员工个个都很庆幸。

C厂长在大会说：今年亏损，奖金不发了，我还要裁人，会后居然有很多员工给C厂长送红包。

为什么同样的问题，人们在不同的表述面前有不一样的决策呢？

因为这是大脑处理问题时发生的认知偏差，正是在这个认知偏差的迷惑下，让我们在当时做出了后来追悔莫及的决定。

心理学上把这种由于不一样表达导致不一样结果的现象叫做「框架效应」。

它是指对同一个问题在两种逻辑意义上相似的说法，却导致了不同的决策判断。也就是说，我们的思维在处理相同问题时，总会受到不同表述框架的影响，从而做出不一样的决策。

那么，我们面对问题作出决策时为什么会被囿于框架之中呢？

这是因为思维处理问题的过程中，会自动使用问题本身呈现出来的语境信息，并把这些信息进行语境化处理，根据这个处理结果进行决策。

整个思维处理过程如下图：

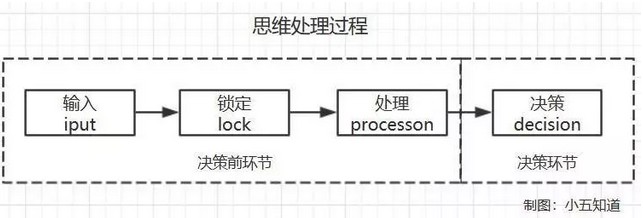
在审视这个语境化处理过程时，不难发现它可以分为决策前处理的输入、锁定、处理环节和决策环节两大处理阶段。

那么，这两大环节在框架效应中分别起到什么作用呢？

输入、锁定、处理等决策前环节是处理问题时逐步形成框架的环节，决策环节则是基于框架得出结论的环节。

下面我们探寻下信息从输入到锁定再到处理的这个过程中，思维究竟发生了什么使得它最终形成了框架影响决策。为了进一步解释清楚这个过程，我们不得不认识影响这三个过程的2大原则和1个诅咒，即真实原则、接受原则和知识的诅咒。

一、输入时遵循真实原则

我们很少怀疑问题本身，在没有任何干扰的情况下，思维会自动将问题归为它本身描述的样子，并且认为这种表征为「真实」，最终依据这种真实表征来框定思考范围。

心理学家经过多年研究告诉我们：人们只关注正面情况，而不表征也许非真的事件状态。

约翰逊·莱尔德（Johnson Laird）在「心理模型理论」中强调：

很多推理错误来源于没有表征其他结果和假设。

在心理模型理论中诸多表述中，「真实原则」强调人类的心智倾向于只表征真实状态（即问题呈现出来的语境状态），但不表征非真状态（即问题题面之外其他言外之意），以便使自己的工作记忆负担最小化。

这样的例子不胜枚举：

某房地产商说首付2折，日还房贷56元。（用「日还」的概念让你会觉得一天才还那么点，这个楼盘的房贷真的很低。）

卖牛肉面的服务员在你点完餐后会问一句：加肉还是加蛋？（用加肉还是加蛋让你感觉，加肉或者加蛋是个很正常的行为）

二、锁定时遵循接受原则

基于真实原则的前提下，人们在接受问题时就倾向于接受问题呈现出来的框架，并且在问题的框架下处理问题。在人们潜意识里会认为，描述具有不变性，程序也具有不变性。这就是「接受原则」。

我们先说描述不变性，思维处理问题时为了减少负荷总会认为问题的描述具有唯一性，不可随便更换。

接着说医生治病的例子，当病人接受了10%的死亡率时就被这个表述框定，在没有外力的干涉下，大部分人不会自己醒悟在10%的死亡率背后，还匿藏着一个90%成功率的描述，而这个描述是那么的阳光积极。

诸如「话又三说，巧说为妙」、「三思而后行」等众多俗语，都在告诉我们描述不一致带来的不同效果。总之，你对一个四十岁的女人说风韵犹存，要比徐娘半老要让她舒服很多。

我们再说说程序不变性，思维认为处理问题遵循的程序具有不变性。这一原则告诉我们：偏好引发的方式不应该影响选择。

我们在听到服务员问我们面里要加肉还是加蛋的时候，只会下意识地回答加肉或者加蛋，其实我们完全可以什么都不加。

三、处理时难逃知识的诅咒

知识的诅咒是奇普·希思（Chip Heath）和丹·希思（Dan Heath）在《让创意更有粘性》一书中，提到的一个心理学概念。它指一旦我们知道了某事，就无法想象不知道这事的情况发生的原因，我们的知识诅咒了我们。

遭遇知识的诅咒时，我们经常会有一种用已知知识对问题进行语境化处理的适应倾向，毕竟在自然状态下大多数的已知知识都是对的。

我们来看看下来两组描述，请问他们表述是否正确。

描述一：

所有人都会死，黑人会死，所以黑人是人。

描述二：

所有植物都需要阳光，老鼠需要阳光，所以老鼠是植物。

大部分人认为描述一没问题，而描述二是错误的。但我们仔细分析之后会发现，这两个描述都是错的。之所以知道描述二是错的，更多的是因为大家都知道老鼠是植物这个知识本身就是错的，而之所以认为描述一是对的，因为已有的知识告诉我们黑人是人，这就是知识的诅咒。

那么，通过上面三个步骤，思维已经被画出了一个明显的框架，下来我们说说做决策时又是如何被这些框架影响的。

我们先试想一个情形：

有两家相邻的面馆，面分量一样，价钱一样，味道也不相上下。唯一不同的是A店的碗大面只能装个碗底，而B店的碗小则每次都能装满。请问，你觉得哪家面更划算？看到这样的表述你可能会说一样划算。如果你分别去两家面馆吃一次饭，你肯定会说：A店才给人一个碗底，B店却是满满一碗。

四、前景理论

这里我们需要再介绍一个新的理论——「前景理论」，这是诺尔贝奖得主丹尼尔·卡曼尼（Daniel Kahneman）和合作伙伴阿莫斯·特沃斯基（Amos Tversky）明确提出，人们在面临风险决策过程中表现与传统期望值理论和期望效用理论不一致的行为。

前景理论指出：在不同的风险预期条件下，人们的行为倾向是可以预测的。一般情况下，人们在获得收益时总小心翼翼，而面对失败时都愿意冒更大的风险；此外，人们在面对等量的损失和获得时，损失带来的痛苦要远远大于快乐。

在具体执行过程中，前景理论将有以下五种预测方式。

1. 确定效应

人们在面对确定性收益和概率性收益时，多数人会选择确定性收益。这种「见好就收，落袋为安」的方式被称之为确定效应。

我们来做个实验：

你现在有这么两个选择，A你可以获得50000元，B你有70%的可能性获得60000元，30%可能一分钱也得不到，你会如何选择？

在这个实验中，大部分人选择了A直接获得50000元，即使选择B可能获得的更多。

2. 反射效应

人们在面对损失和概率性损失时，多数人会选择概率性损失，这种为了减少损失「赌一把」的方式被称之为反射效应。

我们来把确定效应中的实验做个变异：

你现在必须面临这么两个选择，A你一定会损失50000元，B你有70%可能性会损失60000元，30%的可能性一分钱也不损失。你会如何选择？

在这个实验中，大部分人选择了B想堵上一场，哪怕最终损失更多也不愿意破财免灾。

3. 损失规避

人们在面对同等量的损失和收益面前的敏感程度是不对称的，面对损失的痛苦要远远超过获得收益的快乐，我们将这种现象称之为损失规避。

经济学家经常会通过一个赌局来论断这一观点：

假设投一枚质地均匀的硬币，正面为赢，背面为输，如果赢了可以获得50000元，输了失去50000元。请问你是否愿意赌一把？请做出你的选择。

在这个期望值为零且绝对公平的赌局中，大部分人为了规避损失选择不玩这个游戏。

4. 参照依赖

人们在做判断时往往会选择一个参照点，我们将这个现象称之为参照依赖，我们在本小节开始举得面馆的例子就证明了这一点。

5. 迷恋小概率

人们对小概率事件也有着无限的热衷和迷恋，购买彩票就是一个很明显的例子。

五、如何避免框架效应？

那么，如何才能避免我们堕入框架效应的牢笼呢？

根据决策步骤，我们至少有4次机会让决策最优化，从而避免掉入框架效应作出后悔莫及的决策。

1. 输入时学会假设

对输入内容进行质疑，寻找问题表述的「非真状态」，把表征描述从锚定的世界里拉出来，并重新表征一种虚拟的状态。当思维表征与真实状态不同的虚拟状态时，就可以进入下一步了。注意这里的虚拟状态不止是一种状态，一个问题的非真状态可能有多个，所以要尽可能多的去寻找非真状态。

2. 锁定时探索新框架

对第一步虚拟出来的各种非真状态做出新的框架，扩大原来问题描述的框架限定，根据非真状态的数量获得相同数量的新框架结构。思维过程中可通过改变描述的方式或者改变程序的方式，探寻尽可能多的新框架。

3. 处理时趋向陌生化

对所有框架（包括问题真实状态的产生的框架）内的知识进行陌生化处理，陌生化处理常用的方式为去意境化，让第二步产生的框架不受已有知识、熟悉语境的困扰。

4. 决策时选择最优方案

截止第三步思维已经对信息进行了完整处理，这时根据「前景理论」对每一个方案的寻找多种决策，并对每一种决策进行对比，最终选出最优方案。

经过这样一系列步骤之后，你做出的决策才会是最优决策，才会最大程度的避免决策失误，不至于产生太多追悔莫及的决定。

最后还是那句老话，记住：坚持去做，比什么都重要！

作者：陈小五，微信公众号：小五知道（id：cxwshow）

本文由 @陈小五 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自 Pixabay，基于 CC0 协议