编辑导读：对于经常需要用数据、做分析、理逻辑的投资者来说，数据可视化是一项利器。它能够帮助我们快速发现规律、找到原因，做出判断。如何使用数据可视化呢？本文将从可视化方案的五大类进行分析，希望对你有帮助。

上次屠夫以《可视化的意义》开启了数据可视化系列，解答了3个问题：

• 「数据」可以用来做什么？
• 「分析」能解决哪些问题？
• 「可视化」的意义是什么？

今天，我们将推进到「可视化的使用」，帮大家更好地理解这个工具。

一、可视化方案该怎么选？

上一节课里，屠夫总结过：

• 可视化可以辅助分析过程的推理
• 可视化可以辅助分析结果的表达

一方面是过程，一方面是结果，看似泾渭分明的两部分，在实际的数据分析工作中是相辅相成的。

许多时候，我们做数据分析是带有探索和挖掘性质的，上一阶段的分析结果可能会成为下一阶段分析的方向。选出合适的可视化方案，不但有助于表达当前阶段的分析结果 (承前)，还有助于开启下一阶段的分析思路 (启后)。

想在数据分析中选出合适的可视化方案，得先了解我们的“选项”都有哪些。可视化的图表数量繁多，再加上可以使用的元素组合 (比如色彩)，可谓千变万化，逐一列举自然是不可能的。但是，可视化方案其实可以归纳为「D·R·C·C·T」5大类。只要熟知这5大类，就能做到对数据可视化应用自如。

二、Distribution · 分布

第一大类是D · Distribution，分布。

如果要选出自己最常用的可视化类型，屠夫的答案一定是「分布」。分布之于可视化，就如清蒸之于烹调 ——方法不复杂，但最大限度地保留了食材的本来味道。它以最原汁原味的方式展现数据特征，让我们对分析对象有初步认知。

「分布」类可视化的典型代表包括散点图、直方图和箱线图。这3种分布类可视化，其实我们在中学课程里都学过，但大部分人都低估了其作用。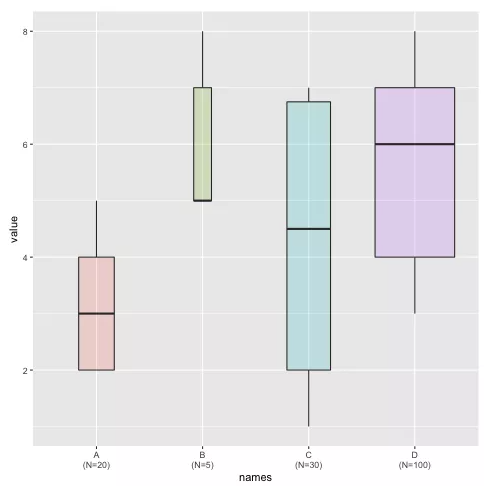

来源：r-graph-gallery.com

比如这一张简单的箱线图，其实把4类数据的最小值、25%分位数、中位数、75%分位数、最大值和样本量 (箱子的宽度) 全部展现在我们眼前：

1. 考虑样本量的多寡：D类最多，B类最少……
2. 考虑value值的离散：B类最集中，C类最分散……
3. 考虑value值的大小：A类最大者小于B类最小者……

「分布」类可视化方案中也有一些不常见的图表，比如屠夫曾在《给我3枚硬币》用过的平行坐标系：

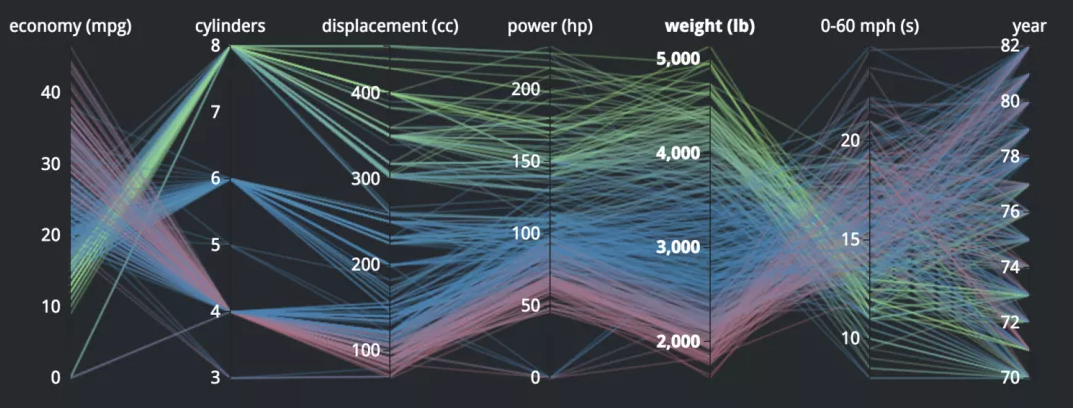
来源：columbia.edu

上面的平行坐标系展现的是上世纪70、80年代的32款汽车在每加仑汽油行驶的里程 (mpg) 、气缸数 (cylinders) 、引擎大小 (displacement) 等维度下的分布情况。可以看出，当时的汽车气缸数分布比较集中 (4、6、8)，但是车身重量 (weight) 的分布却非常分散。又比如上半年大家经常看的地理热力图 —— 结合地图和颜色后，以简单清晰的方式把数据分布展现出来：

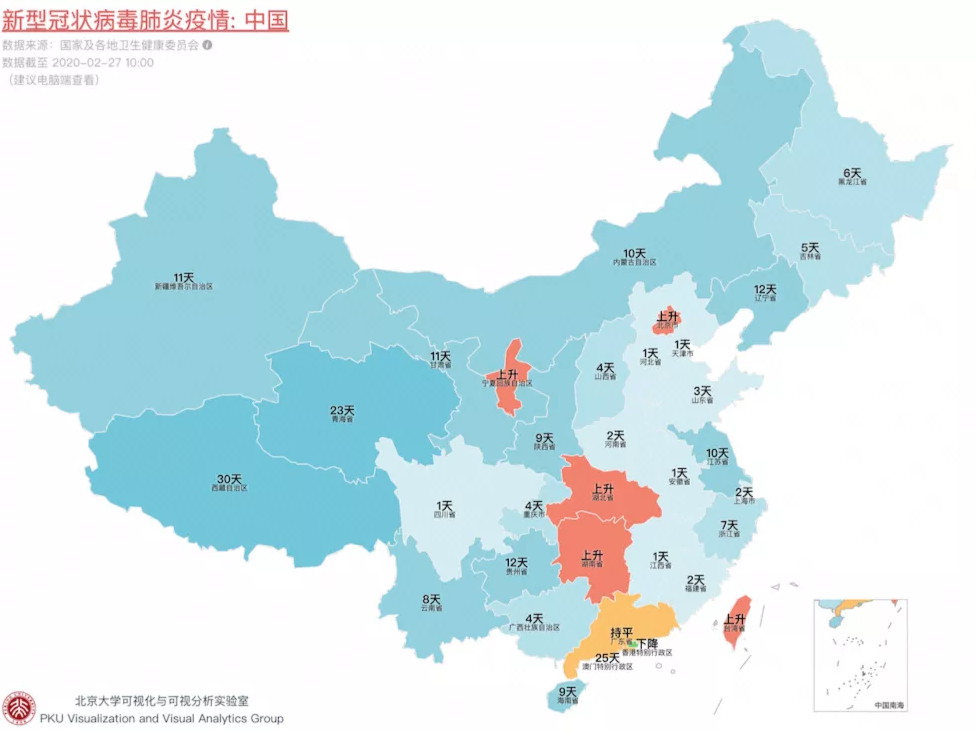
来源：北京大学可视化与可视化分析实验室

「分布」类可视化，是解决数据分析问题的良好开端。屠夫并不指望这类可视化能获得最终答案，但却是迈向最终答案的第一步。一份数据集到手，无论分析的目标是什么，先看看分布，准没错。

三、Relationship · 关系

第二大类是R · Relationship，关系。

「关系」类的可视化方案，侧重展示的是数据的相关性和关联关系。从广义上说，任何一类可视化都可以通过添加“系列”实现展示数据的关系  (如果有的话)。

比如上面的例子，将多类数据的箱线图放在一起，可以展示「分布」方面的「关系」；又比如，将多类数据的饼图放在一起，可以展示「构成」方面的「关系」；再比如，将多类数据的折线图放在一起，可以展示「趋势」方面的「关系」。

在实际应用中，屠夫还是习惯将“「关系」类可视化方案”定义缩小一点，归纳为“基于坐标系”和“基于图”两种。基于坐标系的「关系」类可视化方案，包括散点图、气泡图、六边形分箱图、热力图和平行坐标系等。六边形分箱图和平行坐标系的使用比较少，热力图在上一节已经提过，这里介绍一下气泡图。气泡图可以理解为散点图的加强版 —— 将点换成圆，以圆的面积 (注意，不是半径) 多展现一个维度的信息。

下面是一个气泡图的例子，作者加上了趋势线来表达气泡数据的相关性：

来源：instagram.com

基于图的「关系」类可视化方案，包括力导向图和弦图。力导向图的名字比较拗口，如果屠夫说“关系链”，许多人应该会“哦”地一下恍然大悟。力导向图用节点代表对象，用连线代表对象之间的关系。比如下面的力导向图表达了抽象派艺术家们的社交关系，不难看出，关系网中最有影响力的关键节点是毕加索：

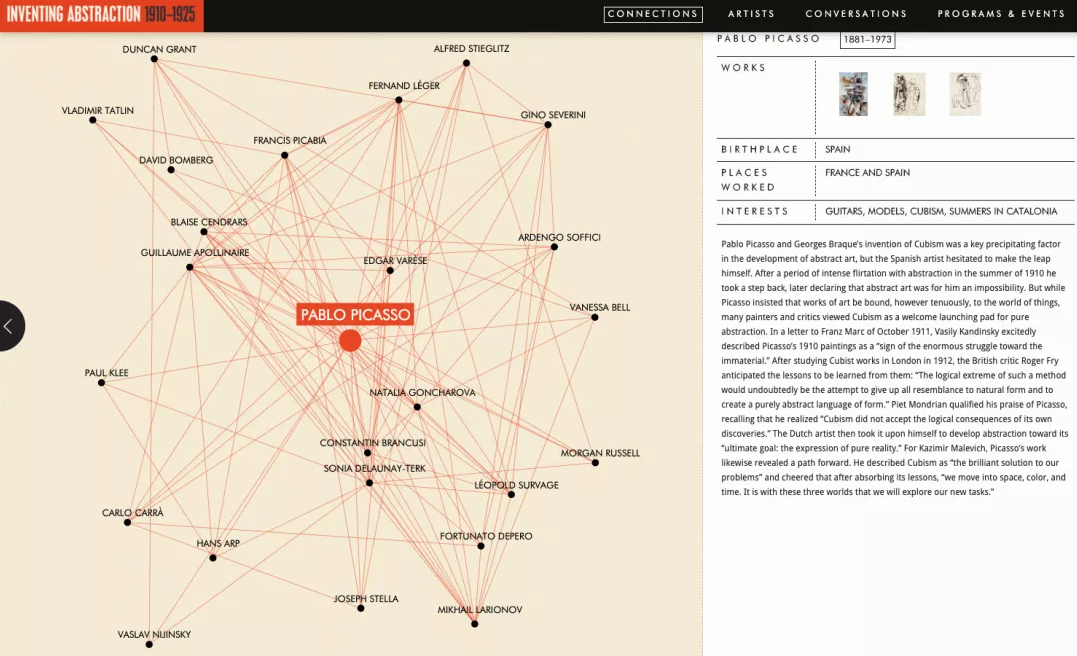
来源：moma.org

弦图则显得更优雅一些 —— 将圆的每一段表示一个对象 (相当于力导向图中的节点)，再用贝塞尔曲线表示对象之间的关系 (相当于力导向图中的直线)。下面的例子是以弦图展现海外一些期刊之间的引用关系，屠夫选择观察《Science》的引用/被引用关系：

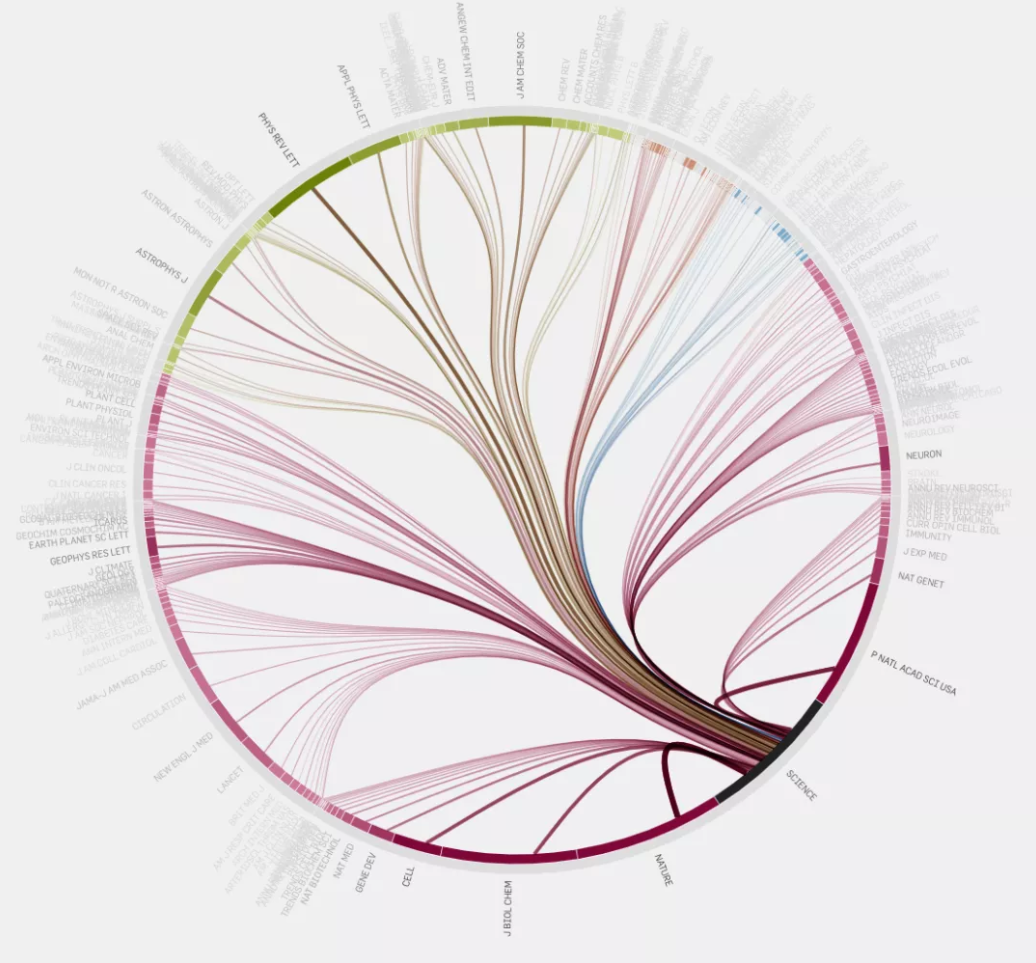
来源：well-formed.eigenfactor.org

四、Comparison · 比较

第三大类是C · Comparison，比较。

「比较」类的可视化方案，重点在于不同数据之间的对比、突出差异点，和「关系」类的可视化方案正好是不同的出发角度。这类可视化方案一定绕不开的典型代表，是柱状图。屠夫在考察候选人的可视化功底时，必问的一道题是：直方图和柱状图有哪些区别？

我说的当然不是名称上的区别 (Histogram V.S. Bar Chart) ：

• 从应用角度，直方图常用于「分布」，而柱状图常用于「比较」
• 从数据角度，直方图适用于连续型变量，而柱状图更适合离散型变量
• 从制图角度，直方图的直方无间隔，而柱状图的柱形有间隔

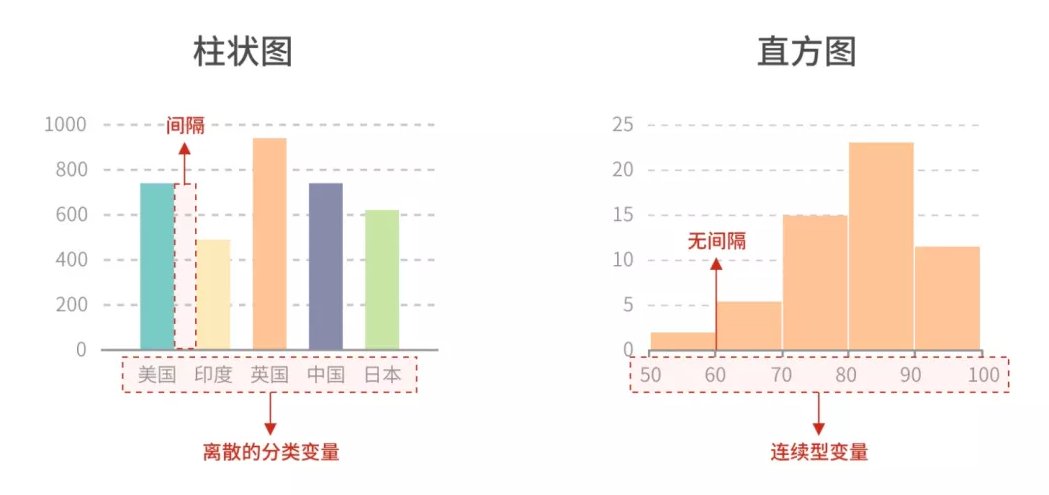
来源：图之典柱状图的应用很广泛，看起来似乎很枯燥。其实只要做简单变化，柱状图的视觉效果也可以很惊艳，比如下面这张将柱状图和极坐标系结合的图表：

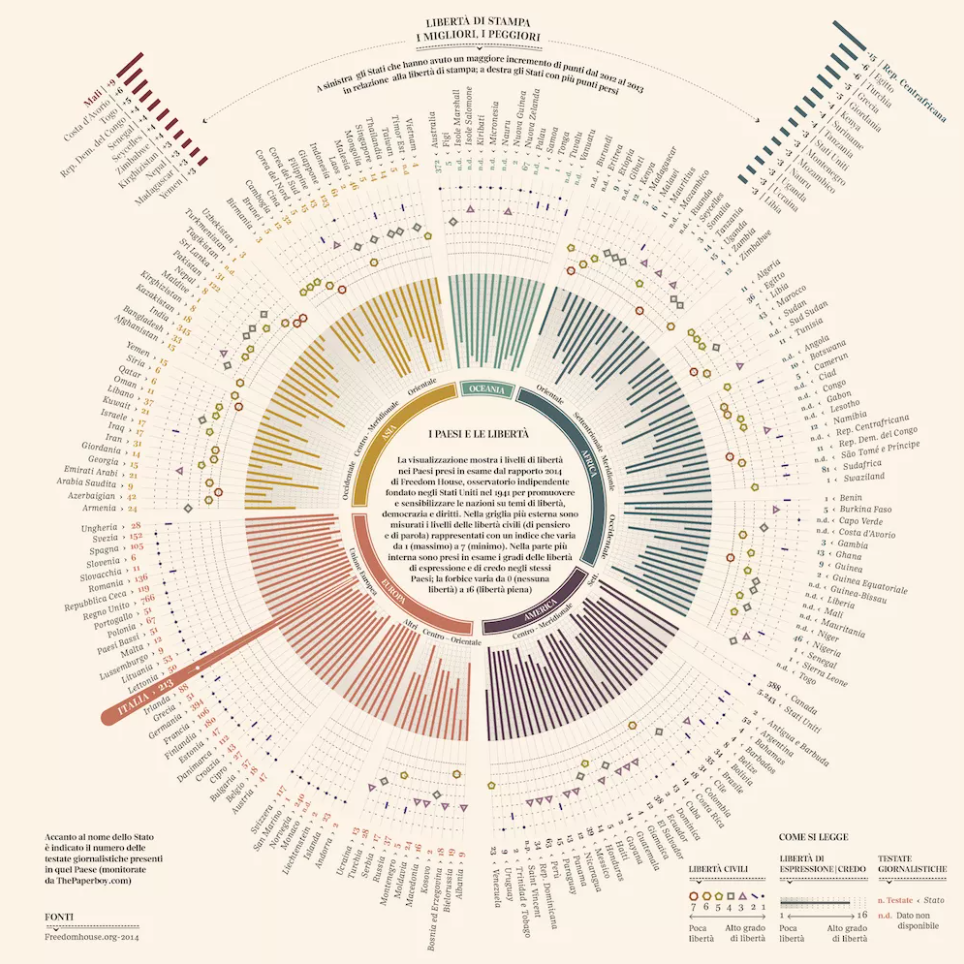
来源：behance.net

适合「比较」的图表还有很多，包括上面提到过的热力图、气泡图等等，这里屠夫还想再举的一例是雷达图。雷达图在许多游戏中出现，常表示人物的多维度属性或者能力值。既可以对比同一人物的不同维度，也可以对比不同人物的同一维度，看起来简洁而直观。

下图是基于2013年NBA全明星球员绘制的雷达图：

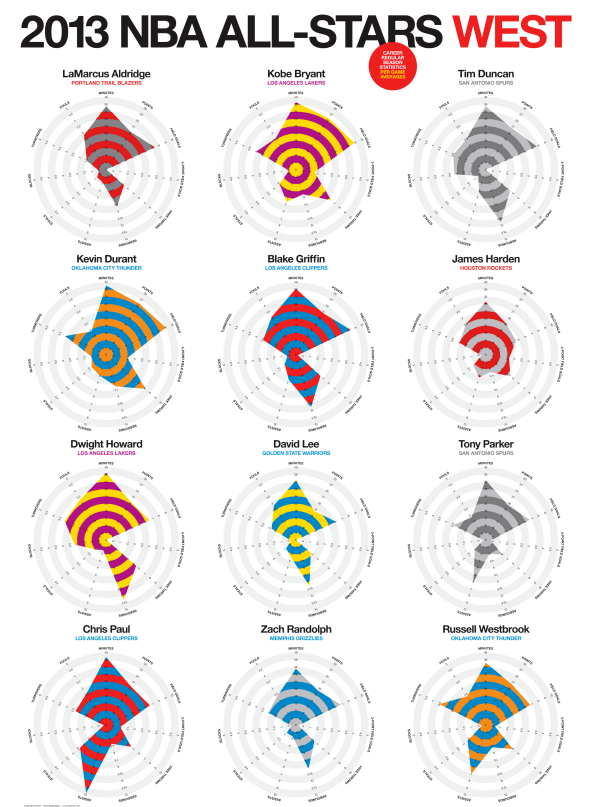
来源：fastcompany.net

五、Composition · 构成

第四大类是C · Composition，构成。

「构成」类的可视化方案，重在展现整体里的构成比例，最简单的「构成」例子非饼图莫属。或许有同学会问，饼图也展现了不同部分的大小比例，是不是也可以和柱状图一样，作为「比较」类的可视化方案呢？

理论上可以，但屠夫不建议这么做。人眼对于面积和角度的感知敏感性远低于长度，而饼图恰恰是运用面积和角度进行可视化表达，在「比较」方面不够显著。

举个例子，下面3种情形属于“比较对象的数值接近”，我们从上面饼图里获得的对比效果，远不及下面的柱状图—— 虽然上下两张图，是基于相同数据绘制的。

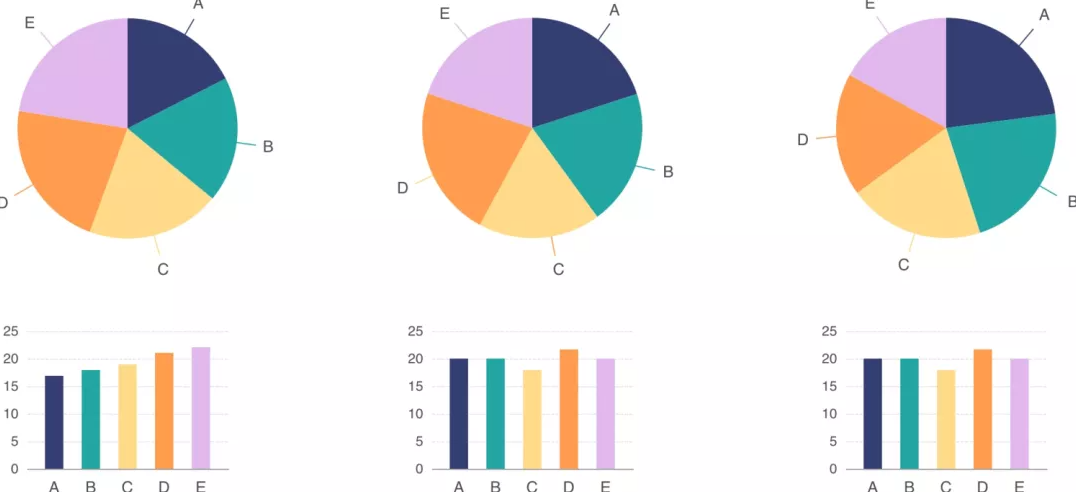
来源：图之典

实际分析里我们也会遇上“带层级结构的数据”，这时我们需要饼图的加强版 —— 旭日图。旭日图又叫“多层饼图”，以同心圆的多层来表示层级关系，内层是外层的“父”，本质上也是一种树状结构。

比如下面这张图展示了不同咖啡风味的层级关系：

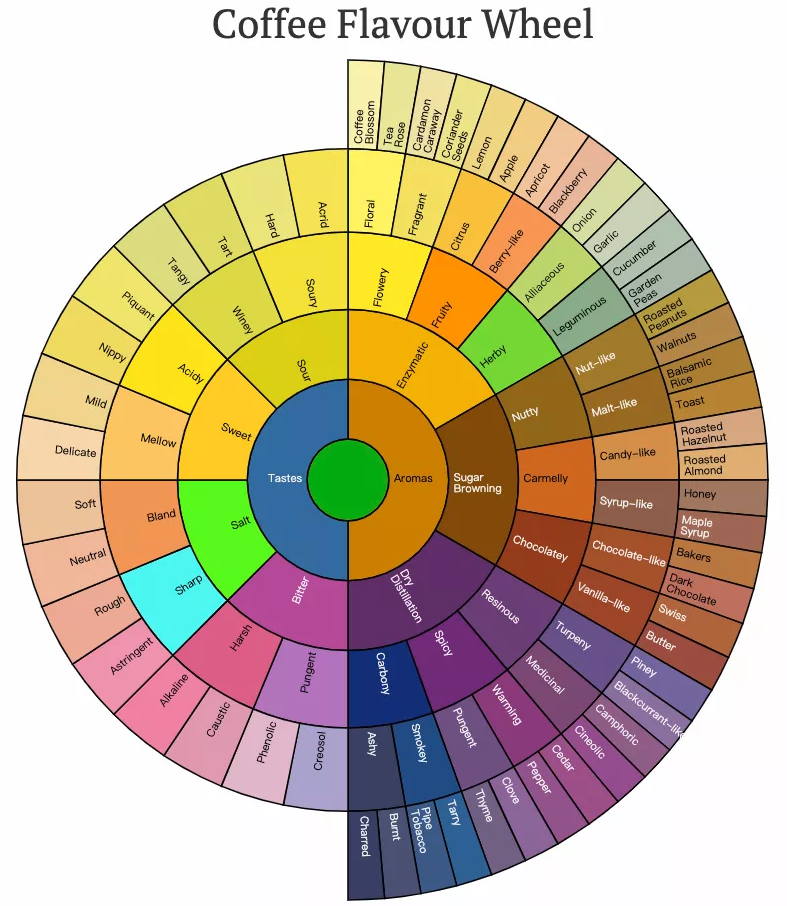
来源：jasondavies.com

较真的同学会发现，饼图运用了圆的“圆心角”，旭日图以此为基础套上“同心圆”，却没有发挥“半径”。如果把圆的半径也用于数据表达，就会形成南丁格尔玫瑰图。顾名思义，这是由著名的医疗改革家南丁格尔护士发明的一种图表，用扇形的半径来表达数据。

下面的例子是Facebook在2016年的用户画像，每一块扇形表示一种数据维度，而人口统计学属性 (性别、收入、年龄、学历) 还使用了层叠：

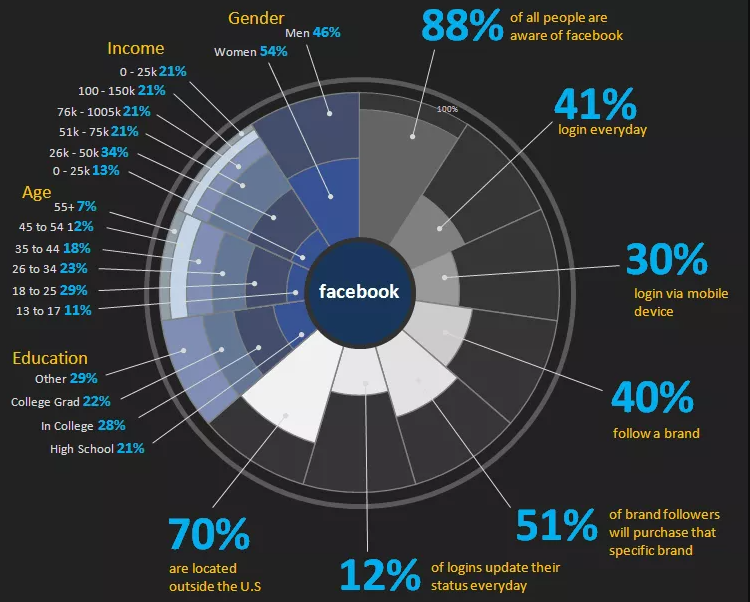
来源：excelhowto.com

六、Trend · 趋势

第五大类是T · Trend，趋势。

「趋势」类的可视化方案，重在描述数据随某一维度变化而变化的情况。“某一维度”往往是「时间」，这样的图表就是我们经常见到的折线图了：

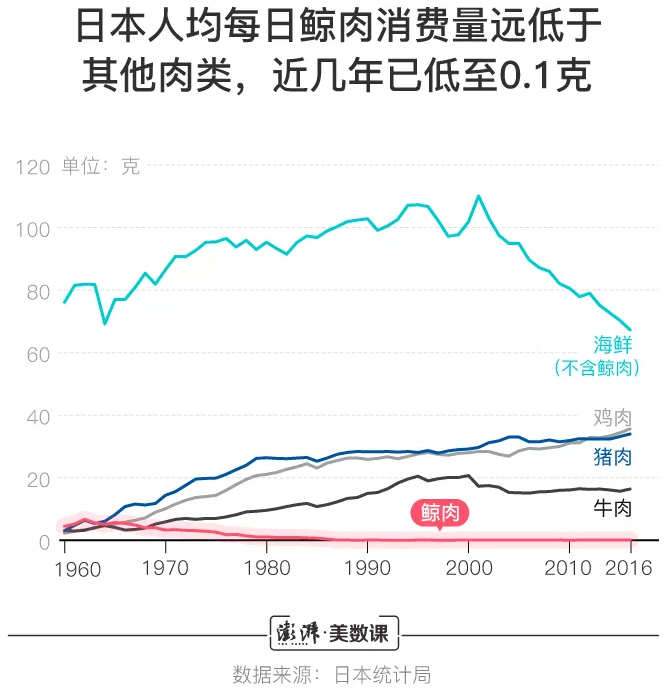
来源：澎湃新闻

注意了，屠夫只是说“往往是「时间」”，总会有例外。如果“某一维度”是「流程节点」，那么可以用桑基图来表达：

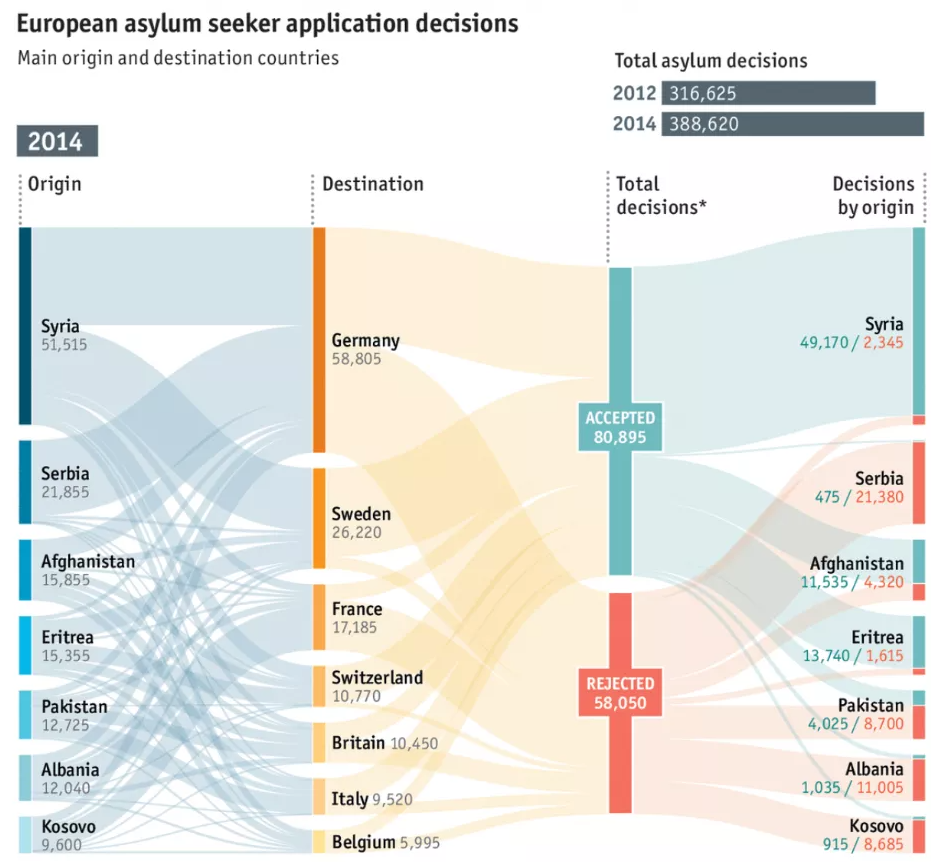
来源：经济学人

上图是经济学人对“难民流向”问题的可视化，其中蓝色表示难民来源国家，黄色表示迁移目的地，绿色表示成功入境，红色表示拒绝入境。

桑基图在互联网行业常用于用户路径分析，每一个节点可以表示一个功能页面，而节点间的条状带表示有多少用户沿着这个方向跳转或流动—— 这，也是一种“趋势”。

把桑基图顺时针旋转90度，再挑选其中一种路径进行展示，就成了另一种图表 —— 漏斗图。依然是来自经济学人的可视化案例，这次是有关职场性别歧视 (薪资差距) 的分析，对比同类型工作中男女薪资差异。

漏斗从上至下分别是：

• 所有工作
• 同级别的工作
• 同级别且同公司的工作
• 同级别、同公司且同部门的工作

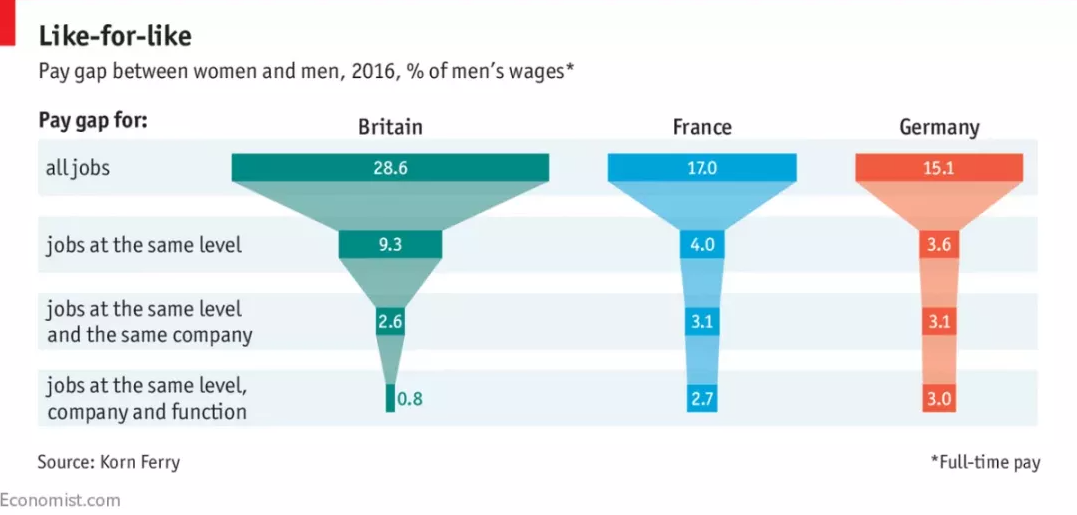
来源：经济学人

七、可视化方案5大类的总结

无论是在分析过程中辅助推理，还是在分析结果上辅助表达，选取合适的可视化方案十分重要。

让我们重新回顾一下5大类可视化方案及其作用吧~

【Distribution · 分布】 展现数据的分布情况，是洞察的基础【Relationship · 关系】 表达数据之间的关系，突出的是关联【Comparison · 比较】 对比数据的不同表现，重点的是差异【Composition · 构成】 呈现数据内部的成分，关注的是比例【Trend · 趋势】 考虑数据随时间、流程等维度变化的情况在第二节课的最后，屠夫整理了一些常见图表的可视化功能，大家不妨保存下来随手查询哦~

作者：屠夫1868，微信公众号：基业长红

本文由 @屠夫1868 原创发布于人人都是产品经理，未经作者许可，禁止转载。

题图来自Pexels，基于CC0协议。