之前在[HCI] 談人機介面設計與Usability 一文中提到了usability的概念，並用了Windows的開始鈕說明了在設計UI上容易忽略的陷阱。這篇文章我會繼續探討介面設計與usability，並以效率(Efficiency)與UI設計時最重要的定律之一費茲定律(Fitts’-Law)為重點。

設計軟體的操作介面並不難，但很多時候直覺的設計並不一定能達成想像中的目的。這就是usability的研究想要了解的，到底什麼樣的設計才是「更好」的設計？什麼樣的設計其實只會讓usability變得更糟？

以menu bar為例，menu是圖形介面(GUI)的最基本元素之一，現代軟體功能越來越強大，包山包海的結果就是menu變得越來越多、越來越深，每一個 menu展開後幾乎都有sub-menu，甚至還有sub-sub-menu等等複雜的選單。我每次教我爸媽用電腦時，都覺得Windows的menu根 本是設計來折磨使用者的，奇妙的是竟然很少聽人在抱怨這介面很難用，而是紛紛強迫自己「學會」這種操作模式。

我想會看到這篇文章的讀者，早就很習慣於操作GUI了，也沒想過選單能有什麼好用或難用之別。所以先讓我們來想想要開啟一個埋藏在sub-menu 裡的功能是多困難的工作（就假設是檔案/最近開啟/某檔案.txt好了）。第一，把游標移到menu bar的「檔案」上，並停住不動；第二，按下滑鼠左鍵打開檔案選單，把游標「垂直往下」移到「最近開啟」上停住；第三，等sub-menu打開，把游標 「水平往右」移進sub-menu裡；第四，再度「垂直往下」找到某檔案.txt，在上面停住並按下左鍵。好，想像完畢後你可以試著用你的非慣用手操作滑 鼠做一次看看。

如果是已經很熟悉GUI的使用者，想必都不覺得操作選單有什麼困難的，但當你被迫用非慣用手操作時，一定會感覺到操作速度大大的降低，甚至沒辦法精 準控制游標進入sub-menu，這時我們才有機會體認到操作滑鼠其實並不容易。除此之外，如果仔細觀察，還可以發現進入sub-menu又比平常把游標 移到任意地方還困難，因為必須把游標保持在一條狹長的「隧道」裡水平移動，如果在移動時不小心移出了這條隧道，sub-menu就會關閉。

有個有趣的案例發生在一個著名的open source影像處理軟體GIMP上（可以說是免費版的photoshop）。當初開發GIMP的團隊曾做過一個有趣的決定，他們決定拿掉固定在視窗頂端 的menu bar，並用可以在任何地方按右鍵打開的context menu取代。因為context menu可以在任何地方打開，GIMP的開發團隊認為這樣可以加快存取menu的速度。這個想法很直覺，但真的對efficiency有幫助嗎？

既然我都說了這麼多，答案當然不會是yes。

context menu對efficiency並沒有幫助，反而使之變得更差。為什麼呢？

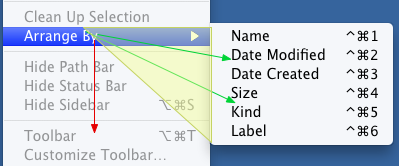
如上圖，從第一層的選單要進入第二層時，必須先經過第一層狹窄的隧道(紅色區域)，才能進入第二層選單。如果直接走直線路徑到想要按的目標，就會先 經過第一層的其他項目，導致不同的sub-menu被打開。傳統的menu bar也是有sub-menu，所以直覺上可能不會覺得多一層的sub-menu會有多大影響，但事實上是這種把游標限制在一條隧道裡的設計大大的降低了 操作游標的速度，和一般可以經由任意路徑指到目標的操作有指數級的速度差異。

Fitt在1954年提出了Fitt’s Law，可以說是人機互動領域的第一條「定律」，對人類指向任一目標的動作建立了一個數學模型。基本的概念是，移到目標上的時間(T)可以表示為目標距離(D)與目標大小(W)的函數。具體來說，T = a +b log₂ (D/W+1)，a和b都是一個常數。

Fitt’s Law告訴我們，移到任意目標上的時間大約跟目標距離除以目標大小的對數成正比。也就是說，目標越遠移動時間就越長，目標越小時間也會越長；反之，目標越 近或目標越大的話，所需時間就越短。有趣的是，距離和目標大小的影響並不算大，經過log讓這兩個變數的影響降低了一個指數等級。例如距離變長1000 倍，並不會讓時間也變成1000倍，而是變成log₂ (1000)，大約是10倍而已。

在軟體介面上，Fitt’s Law有個特例值得討論一番。在電腦裡的滑鼠游標，有個基本特性是其活動範圍被限制在螢幕裡，只要游標到了螢幕邊緣，無論再怎麼繼續往同一個方向移動滑 鼠，游標還是只能停留在邊緣上。這個特性讓UI設計有了戲劇性的變化，一個最有趣的例子是Windows和Mac OS X的menu bar設計。

Microsoft的Windows自古以來的UI設計都是把menu bar放在視窗的title bar下面，而Mac OS採取完全不同的設計：把menu bar固定在螢幕最頂端。一般人大多覺得這兩種設計只是習慣問題，沒有什麼客觀差別，但如果你已經學會了Fitt’s Law，你覺得哪一種設計比較好呢？

如果直接套用Fitt’s Law，第一個得到的答案很可能會是Windows的設計比較好，因為當滑鼠從視窗內移往menu bar時，距離會比移到螢幕頂端還近。可是，別忘了考慮螢幕邊緣所造成的影響。Mac把menu bar放在螢幕頂端，雖然距離變長了，但目標的大小也跟著變成了「無限大」。因為螢幕的邊緣會阻擋住游標的行動，於是使用者可以盡情的把用力滑鼠往上一 甩，不用停下來「對準」目標，也就等同於目標的大小變成了無窮大。在Fitt’s Law中，當W是無限大時，整個log函數得到的結果會變成0，也就是說T就會變成一個簡單的常數值a，跟距離或大小都沒有關係了。

如此比較之下，我們就可以發現Mac把menu bar放到螢幕頂端是有其用意在的，因為它大大減少了把滑鼠放進menu bar並對準目標的時間，使用者只要把滑鼠用力往前一移，自然就會進入menu bar裡面了。我在[HCI] 談人機介面設計與Usability 一文中也提過Windows開始鈕的例子，跟menu bar的例子也是相同的道理。

到目前為止，我們已經看過了三種形式的menu。對於efficiency而言，我們知道Mac的設計比Windows的設計還好，那如果和 GIMP的context menu比起來呢? 從Fitt’s Law可以得知，Mac的設計已經達到極限了，無論如何也沒辦法捨去那個常數a，所以我們可以直接來比Windows的設計和GIMP的設計哪個比較差 XD。

前面提過，sub-menu是一種很難的指向操作，除了要把游標移到目標上，還限制了中間經過的路徑在一個隧道裡。在Fitt’s Law之後，Accot and Zhai提出了 Steering law 。 其結論非常簡單，讓游標經過一個寬度W的隧道移動距離D的時間 T = a + b * D / W。換句話說，把移動路徑限制住的話，其移動到目標的時間和一般性移動(Fitt’s Law)所需的時間是指數級的差距，這也就是為什麼電流急急棒可以變成一個有百萬獎金的挑戰，而隨意動動滑鼠則簡單的多。

了解了Steering law之後，再回來看sub-menu的設計，你就會發現sub-menu是一個多不人道的設計。每一層的menu其實都是一個steering操作：垂 直的menu移動比較簡單，因為menu寬度通常都蠻寬的；但每當要水平移動進入下一層sub-menu時，就是一個困難的挑戰，因為這時的寬度變成了 menu item的高度，通常也就是一個字母高而已。和Fitt’s Law不同的是，寬度(W)變小n倍，對時間的影響不再是對數，而真的就是讓時間變長n倍。所以說呢，如果可以迅速又準確進入多層sub-menu的滑鼠 高手，其實也有參加電流急急棒比賽的能力呢！

回過頭來看Windows和GIMP的menu設計，這時就可以明顯比較出來。GIMP把所有的選單操作全都變成了steering操 作，Windows雖然也有sub-menu的問題，但至少第一層還是任意的指向操作，所以就efficiency來說，GIMP的設計其實是一大失 策..。

最後，再順便提兩個Windows和Mac OS X對於sub-menu造成的問題所提供的解決方法。微軟和Apple都知道sub-menu很難操作，所以他們其實都有偷偷的在介面上做了一點貼心的設 計。微軟的方法是，在游標要進入sub-menu時，如果不小心移出隧道外，只要在一定的時間內移回來，sub-menu就不會消失。這個方法其實有些風 險，主要是因為這個「時間」很難掌控。如果這個設定的時間太短，那就沒多大效果；但如果設定太長，使用者如果是真的想要移到別的menu item打開另一個sub-menu，就會覺得系統反應太慢（就是那種頓頓的感覺）。所以，微軟的這個方法其實並不是很有效的解決這問題。

而Apple雖然也是用同樣的方法來sub-menu不要馬上消失，但他們又加上了一個聰明的設計：sub-menu的延遲消失只有在游標到 sub-menu的頂端和底端形成的三角形內有效。換句話說，如果使用者是想進入sub-menu中，他甚至可以直線移動滑鼠進入其中而不會意外打開另一 個不同的sub-menu（只要在設定的延遲時間內移動完成）。而假如使用者是想打開另一個sub menu，那直覺的把滑鼠往下移動就會自然的避開這個三角形區域而避免了「頓頓的」感覺。

在UI設計上，Apple一向是比其他公司用心許多。這種聰明的設計雖然很小（甚至沒什麼人會注意到），但在每天反覆的使用中就能自然減少使用者的 挫折感和提昇操作的流暢度，這也是為什麼我常說Mac有許多貼心的設計，用起來會自然讓人感覺很愉快，而其他系統在UI設計上所下的功夫就明顯不足了。

源地址：http://blog.csdn.net/Like……/4660796.aspx