在一次拍卖中如果所有买家的报价均小于卖家的估价时，则拍卖品不出售由卖家保留，此时卖家的估价就是保留价，也叫底价，全称市场保留价。对于卖家来说，保留价的设置保障了自身利益，那么对于拍卖整体来讲，保留价的设置有什么影响？

一、卖家设置保留价的原因是什么？

1. 不想亏本

对于卖家而言拍卖的东西本身具有一定的价值(成本 )，如果在低于该价值的价格出售( )，则此时卖家的效用：

基于个人理性假设，卖家此时选择保留拍卖品，这里引出拍卖的一个基本假设：个人理性，当拍卖双方都不参与拍卖时，收益为 ，支出为 ，效用：

发生拍卖的前提条件是对所有参与人都有利可图，即

另一个基本假设是在《广告系列：机制设计》里提到过的激励兼容(说真话保障广告系统的持续发展)。

2. 为了增加拍卖时竞价环境的激烈程度，保障卖家收益

尤其是在合作博弈中，买者之间存在合谋(竞价环)，通过合作不断降低报价增加了环中的买家收益，环的运作不会影响环外买家的获得物品的概率函数及期望支付，环中增加的收益来自卖家的损失，此时卖家可以借助保留价的机制来对抗竞价环。

二、设置保留价对拍卖的整体的影响是什么？

1. 拍卖可能不再有效

设置保留价后卖家可能会保留拍卖品，没有分配给估价最高的买家，此时拍卖不再有效，影响了拍卖的社会效应，当然如果是基于私有价值的拍卖那么不会有太多人在意；

2. 竞得者的支付函数可能发生变化

当只有一名买家的报价高于保留价时，在广义二价中，保留价将会改变获胜者的支付价格，假设买家 报价 ： ，且

除获胜者以外最高报价记为：

没有保留价时胜者支付：

有保留价时则支付：

此时卖家收益增加。

3. 保留价有诸多好处，卖家在具体某次拍卖中如何设置保留价

定价太高则拍卖品卖不出去，此时卖家效用为 ；定价太低在竞价不充分时则买家 可能以很低的价格获得物品，此时卖家效用 没有达到预期。

对于广告系统而言，粗一些的做法是根据广告主们的历史竞价情况，取一个使填充率没有明显下降的固定值作为保留价，相对比较简单，一定程度上也可以防止广告主无限下探出价，降低平台收益；精细一些就是针对不同广告主设置不同的动态底价，这对数据和模型的要求比较高，当然广告平台的收益也会相应增加，有本事多赚钱的道理，计算方法涉及到我们虚拟估价。

从计算上讲，动态保留价与固定保留价相比，主要差别在于针对不同的广告主设置不同的价格上，更加精细，千人千面就需要了解广告主的特性及对广告曝光的估价分布。

在《广告系列：最优机制》里，我们提出最优机制的拍卖时竞价的标准不是广告主估价而是虚拟估价，并且解释了为什么使用虚拟估价代替估价的经济学解释，它代表了卖家的边际收益，在一次单品拍卖中把物品配置给边际收益最高者，里面有个隐含假设：

最高的虚拟估价高于保留价，即：

其中， 代表卖家对物品的估价，即保留价 ，同时也是卖家的成本。

在求动态保留价时，我们令 ，即：

解出上式中的： ，就得到针对该买家的动态保留价，从上式可以看出要解出等式必须知道 ，即买家估价的密度函数，这个前提与最优机制时是一致的：

4. 不知道各个买家的估价分布无法针对性的设置保留价和最优机制来最大化卖家收益

这里可能会有个疑问为什么令 ，解出来的 就代表了动态保留价，下面我们说下经济学的解释。

从经济学角度，随着物品供给量不断增加时，边际收益递减，边际成本递增，当，企业利润最大化。在单品拍卖中，虚拟估价 代表边际收益，保留价 代表边际成本，

令 ，即，此时卖家利润最大。

又因为广告拍卖的是曝光，有区别与其他拍卖品，不能长期储存，过后即废，所以在实际操作中有时令

此时上式变为：，即：，可得买家的动态保留价。

下面我们用图可以更加直观的感受下：

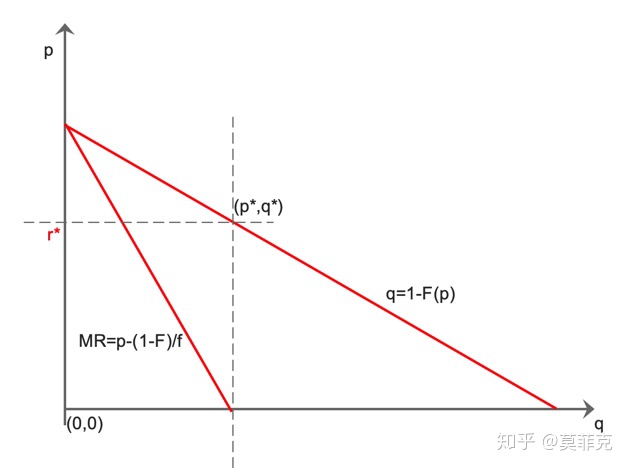
其中， ，代表需求函数， ，代表边际收益函数（也是买家的虚拟估价函数），

当 时，得到最优产量及价格 , 此时 对应上面的动态保留价 。

对于广告系统而言，不同广告主有不同的估价，需要根据历史数据拟合出估价分布函数，基于此求出广告主各自的保留价后分别设置。

这里我们可以完善下关于之前对最优机制的描述：

分配规则：当 时，虚拟估价最高者得，否则保留物品；其中 表示买家的虚拟估价；支付规则：竞得者需支付价为 ，

其中 ，表示除去竞得者买家 的虚拟估价最高者， 表示买家 虚拟估价的反函数，

如果买家是对称的，此时，则：

其中， 表示除竞得者 以外的最高报价。即带保留价为 的二价拍卖为最优拍卖机制。

本文由 @莫菲克 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议