编辑导语：风控模型的应用场景非常广泛，只要牵扯互联网金融的行业就少不了风控，风控模型建好后还要映射到信用分数空间，才能呈现给用户；本文作者分享了详细的建模方法，教你如何建立模型分数，我们一起来看一下。

承接上文《有案例有代码，详细模型分数》本文开头告诉大家怎样更合理的向客户展示信用评估结果。把模型预测值映射到一个分数区间，比如350～950，分数越高信用越好。

很自然的我们就走到了这个最佳选择，至于分数为什么定义在这个区间，我个人理解一是为了跟国际上主流的个人信用评分区间接轨；二是为了拉开用户之间的分数差距。

4. 如何映射分数

最简单最容易想到的是采用尺度变化，将模型预测结果线性的映射到350～950，然后找到cutoff 对应的分数X，告诉用户分数高于X就可以拿到贷款。

等一下！如果过段时间模型更换了怎么办？

模型换了，cutoff随之变化，分数X也跟着变了。这时就会有一部分用户疯狂的呼叫客服问“为啥我的评分变高了，反而不能贷款？”

同时每次更换模型，后台、前端都需要进行相应的逻辑、页面修改，每次模型发布需要多个环节协作完成，是一种高耦合的工作方式。

于是你赶紧召集团队成员讨论解决方案，有人提出一个又简单又好用的方案：分段尺度变换，将cutoff 固定为 680分（本文假定的）然后分成两段作尺度变换。

总结分段尺度变换的优点：

1. 模型切换用户无感。无论模型的cutoff如何调整，用户感知不到差别，只要分数超过680都可以成功申请到贷款；
2. 解耦了模型团队与开发团队。也就是说当模型人员校准好评分后，后台开发只需要设定680分通过，从此以后无论模型人员怎么更换模型，后台开发都不用再重新修改代码。

“`python

predict_desc = table.describe()[‘predict’]

# 这里用几倍标准差确定上下界根据经验设定，是为了避免outlier值使得分数过于集中在某个范围

upper = min(predict_desc[‘mean’] + 5 * predict_desc[‘std’], 1)

lower = max(predict_desc[‘mean’] – 3 * predict_desc[‘std’], 0)

def get_score_linear(predict, upper, lower, cutoff):

“””

将模型打分结果尺度变换到350~950的分数区间

:param predict: float, 模型打分

:param upper: 模型打分上界

:param lower: 模型打分下界

:param cutoff: 680分位置对应的模型打分

:return:

“””

if predict > upper:

return 350

elif predict > cutoff:

return 680 – int((680 – 350) * (predict – cutoff) / (upper – cutoff))

elif predict == cutoff:

return 680

elif predict > lower:

return 680 + int((cutoff – predict) * (950 – 680) / (cutoff – lower))

else:

950

二、客群分层下的分数映射

1. 老用户分层

敏锐的你发现，随着用户的复贷次数增多，原有盈亏平衡点的计算方式会使得拉新成本被计算了多次（用户复贷几次就多计算几次）。

这也就引出了用户分层的一种场景：区分新老客户，分别建模，分别计算盈亏平衡点。

传统的评分卡中A卡B卡也有异曲同工之处：

• A卡用于贷前审批阶段对借款申请人的量化评估，是使用最广泛的；
• B卡用于贷中阶段，增加了借款人的还款及交易行为，预测借款人未来的还款能力和意愿；

综合分析新老用户分别建模的特点：

1. 模型更准确。老客户建模引入了历史还款行为、交易行为，使得模型更准确。
2. 老用户的成本更低。拉新成本归属于边际成本，当新用户转化为老用户后，每多一次复贷都会将拉新成本摊平。那么就可以将拉新成本算在新用户上，老用户的成本得以降低，对逾期率有更大的容忍度；
3. 提高复贷率，提高盈利。修正老客户的盈亏平衡点，可以提高老客户的通过率，从而提高复贷率，提高盈利。

那么我们再重新计算以下老用户的盈亏平衡点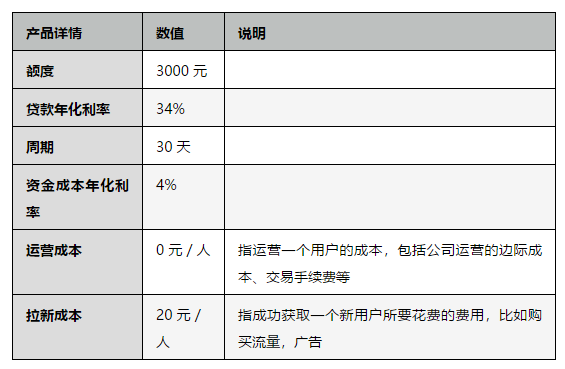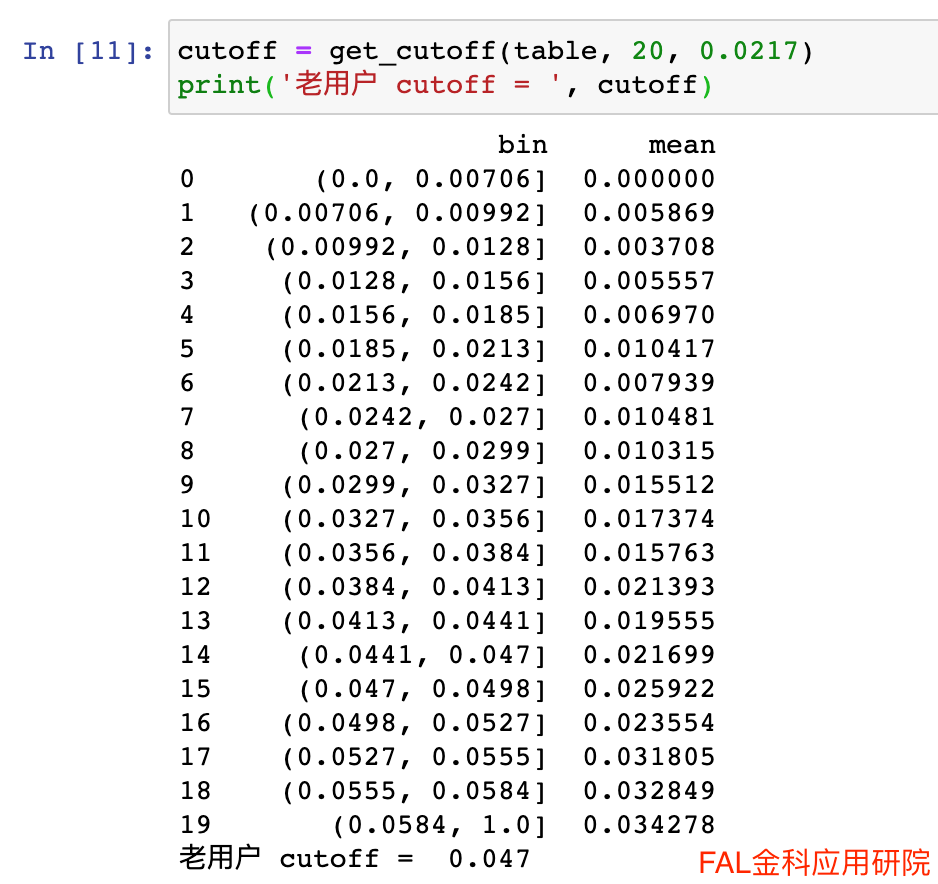：带入公式计算得到盈亏平衡点 pd = 0.0217，在代码中求得cutoff = 0.047。

同理，采用分段尺度变换方法可以将模型结果进一步映射到信用分数空间，这里不再赘述。

此时的你又开始思考如何做大做强。为了吸引更多用户，留住优质客源，你跑断了腿找到一个新的资本方，愿意以更低的资金成本给你提供资金来源。

于是你终于可以上线一款新产品：更低的利率给更好的你。

至此业务进入了多产品轨道。

2. 用户质量分层以匹配不同利率产品

除了按照新老客户性质分层，还可以按照用户质量来划分用户。

将老用户分为优质用户和次优用户，这样做的目的是为优质用户匹配优质产品，更低利率或更高额度。

按照这个思路就可以将用户分为以下四个层次：

• A — 老用户中的优质用户   资金成本0.02 利率 0.22 额度 5000
• B — 老用户中的次优用户   资金成本0.04 利率 0.34 额度 3000
• C — 新用户中的优质用户   资金成本0.02 利率 0.30 额度 3000
• D — 新用户中的次优用户   资金成本0.04 利率 0.34 额度 1000

只以A、B类用户举例，同理带入公式计算盈亏平衡点：

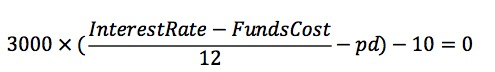
得到：

A类用户盈亏平衡点 pd = 0.01467

B类用户盈亏平衡点 pd = 0.02167

现实业务中可以将ABCD四类用户评级结果直接反馈给用户，比如我们常看到的黄金会员、钻石会员，本质上是类似的；

也可以按照分段尺度变换的思路将分数划分多段，例如：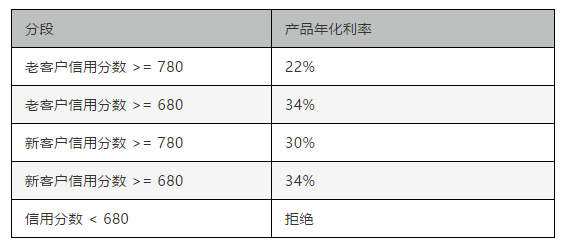

代码可以参考前面二分段尺度变换的代码，增加对应的判断分支即可。

随之而来的问题也就出现了：

1. 如果产品越来越丰富，变换额度、利率，所需要计算的盈亏平衡点越来越多，那怎么办呢？再使用分段尺度变换这种简单粗暴的方法就显得越来越笨拙了，也增加了出错的概率。
2. 当多个模型共同工作或切换备用模型时，如何保证分数尺度一致？这里尺度一致的意思是，两个模型分数相同时对应的逾期率是否一致。

 三、多产品、多客群、多模型下数映射的产生——分数校准

为了能够更好的进行风险定价，业务部门希望模型给出的分数能够准确的反映出真实的信用风险等级。

这一过程称为分数校准(Score Calibration)。

也就是说，我们最终的目标是：建立信用评估分数与预测逾期率的函数关系。

这里介绍一种常用的分数校准方法，通过该方法，可以由分数精准的计算出预测逾期率，反之亦可。

1. 建立Odds与分数的函数关系

熟悉业务的同学会知道，建模时逾期样本非常少，更多的是信用良好的样本。

原因我认为有两点：

1. 现实中好人是大多数的，这点不多解释。
2. 模型长期筛选的作用，通常我们已经得到还款结果的样本是已经通过上一轮模型的一批样本，坏用户已经被上一轮模型过滤掉大部分了。

因此，逾期率与用户数量是符合幂律分布的。也就是说随着逾期率的升高，用户数量呈指数下降。

进而在设计Odds与分数的函数关系时，对Odds取了一个log，再结合简单的线性方程，加入截距A和斜率B进行线性拟合：

也叫做比率Odds，常用来评估风险。（ps：熟悉赌球的朋友会对比率很熟悉），同时有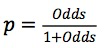

由公式看出来分数与log(Odds)呈线性关系，表示分数每变化多少，逾期率会番翻。

要算出系数A、B的话，需要从业务角度先预设两个前提条件：

我们设定时，应逾期率是0.0196， 当Odds按双倍上下浮动时，分值对应变动100分。

这里设定的值只是为了演示计算，实际业务中应该根据业务情况制定合理的取值。

求解方程组计算得到A，B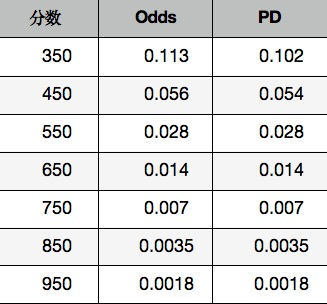

上面这个公式就是分数与逾期率的函数关系，我们可以进一步把分数、Odds、逾期率的对照关系计算出来：

仔细观察我们会发现，随着逾期率PD越来越小，Odds其实近似等于逾期率，这就更方便业务团队进行风险定价。

2. 建立模型结果与Odds的函数关系

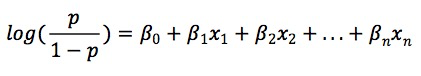
• 对于机器学习模型来说这里变量x可以是一个或多个模型预测结果；
• 对于评分卡来说变量x就是原始特征；

从模型结果到Odds是一个线性回归过程。

至此，我们就完成了一个标准的分数校准。

四、总结

我们回顾一下，随着产品种类，模型数量的丰富，分数映射逐渐有了更多的要求以适应业务的需求和团队协作的高效。

总结一下每个阶段的优缺点：

本文由 @FAL金科应用研院 原创发布于人人都是产品经理，未经许可，禁止转载。

题图来自 unsplash，基于 CC0 协议