编辑导读：假设检验是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法，是统计学中非常重要的方法论之一，有非常广泛的应用。本文作者将以商业机器人行业为例，分析假设检验法在商用机器人业务中的实际应用，与你分享。

假设检验是统计学中非常重要的方法论之一，在实际业务中的应用也非常广泛，生物，医药乃至互联网行业内著名的AB test，其本质都是假设检验。

基于笔者目前所在的商用机器人行业，结合理论和实践，设计了如下的实验，其目的是去论证对于机器人的平均速度的影响因素（由于数据和结论的敏感性，不作披露，希望能够抛砖引玉，将假设检验的方法论应用到更为广泛的业务中）。

一、什么是假设检验

假设检验即小概率反证法，在假设的前提下，估算某事件发生的可能性，如果该事件是小概率事件，在一次研究中本来是不可能发生的，现在发生了，这时候就可以推翻之前的假设，接受备择假设。如果该事件不是小概率事件，我们就找不到理由来推翻之前的假设，实际中可引申为接受所做的无效假设。

理论支撑：

1. 样本来推断总体（需要保证样本的随机性）
2. 中心极限定理可知，当样本数足够时（n>30），样本的抽样分布可近似于正态分布。

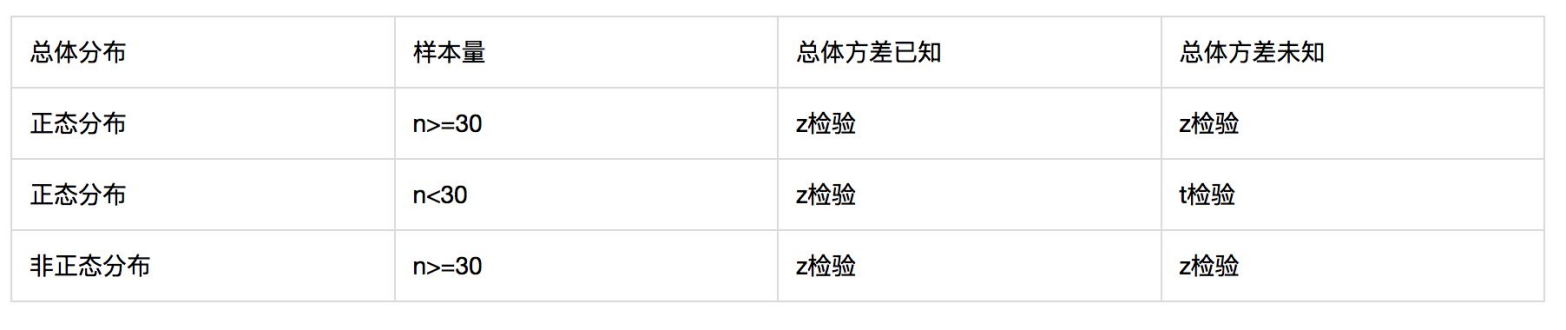
著名的假设检验方法有U（Z检验），T检验，F检验，卡方检验等。这里重点介绍有关平均值参数的假设检验方法：

已知总体方差，用U（Z检验）

如果检验一组样本平均数（X）与已知的总体平均数(μ0)的差异是否显著：

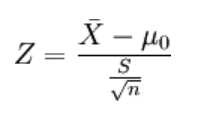
X是检验样本的均值；μ0是已知总体的平均数；S是总体的标准差；n是样本容量。

如果检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著：

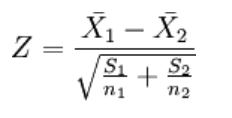
未知总体方差，样本含量较小（例如n<30）且服从正太分布，采用T检验

如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度：

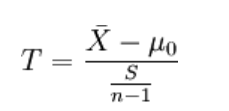
如果要评断两组样本平均数之间的差异程度，其统计量T值的计算公式为：

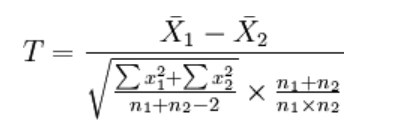
二、实验组

考虑到目前机器人运行速度的整体分布状态未知（简单根据分布图来看，并不能完全判断是正态分布）。所以，现考虑设计以下三组实验记录，再考虑使用Z检验来判断避障/调度是否影响了机器人的平均速度，且该影响是否显著

1. 第一组：同一机器人在完全不发生避障，调度等情况下的成功运行记录（33条）并计算出该33条记录的平均速度u1
2. 第二组：同一机器人在只发生避障情况下的成功运行记录（33条）并计算出该33条记录的平均速度u2
3. 第三组：同一机器人在只发生调度情况下的成功运行记录（33条）并计算出该33条记录的平均速度u3

假设检验一：

原假设（H0）：u1 = u2 （即避障不会影响机器人的运行速度）

备择假设（H1）：u1 ！= u2（即避障会影响机器人的运行速度）

假设检验二：

原假设（H0）：u1 = u3 （即调度不会影响机器人的运行速度）

备择假设（H1）：u1 ！= u3（即调度会影响机器人的运行速度）

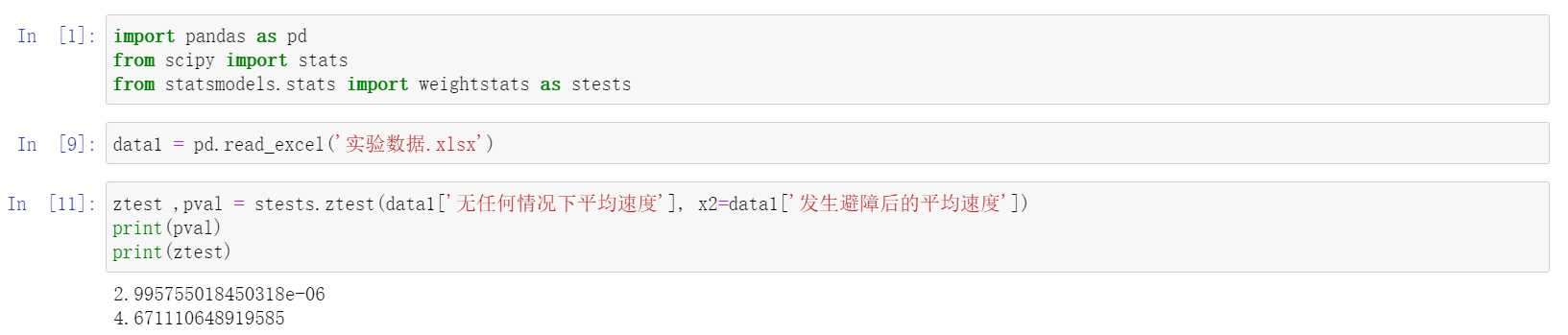
由于是双独立样本，且未知分布，综合考虑采用Z检验，采集数据后，选择相应的scipy函数（https://docs.scipy.org/doc/scipy/reference/stats.html），如果计算出z值远大于1.96，p值无限接近0，几乎不可能发生，即拒绝了原假设，接受了备选假设；否则反之。

三、复盘

如果关于调度，避障之类的影响因素有现成的数据可以分析，其实大可不必线下人工去统计，一是样本量过小；二是人工统计时间，里程等因素费时费力；笔者已将开发这部分数据的需求整理，提交至开发排期。

本文由 @南仔 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议