监督学习（supervised learning），主要解决两类问题：回归、分类，分别对应着定量输出和定性输出。那监督学习中主要的算法模型有哪几种？

我们和小冰聊天的过程，对她来说就相当于很多次的“输入-处理-输出”。从机器学习的视角上来看，小冰在学习怎么跟我们说话的时候（被开发阶段），应该主要采用了监督学习。

监督学习（supervised learning），主要解决两类问题：回归、分类，分别对应着定量输出和定性输出。

什么叫回归（regression）呢？

简单地说，就是由已知数据通过计算得到一个明确的值（value），像y=f（x）就是典型的回归关系。说的很多的线性回归（Linear Regression）就是根据已有的数据返回一个线性模型，大家初高中学了那么久的y=ax+b就是一种线性回归模型。

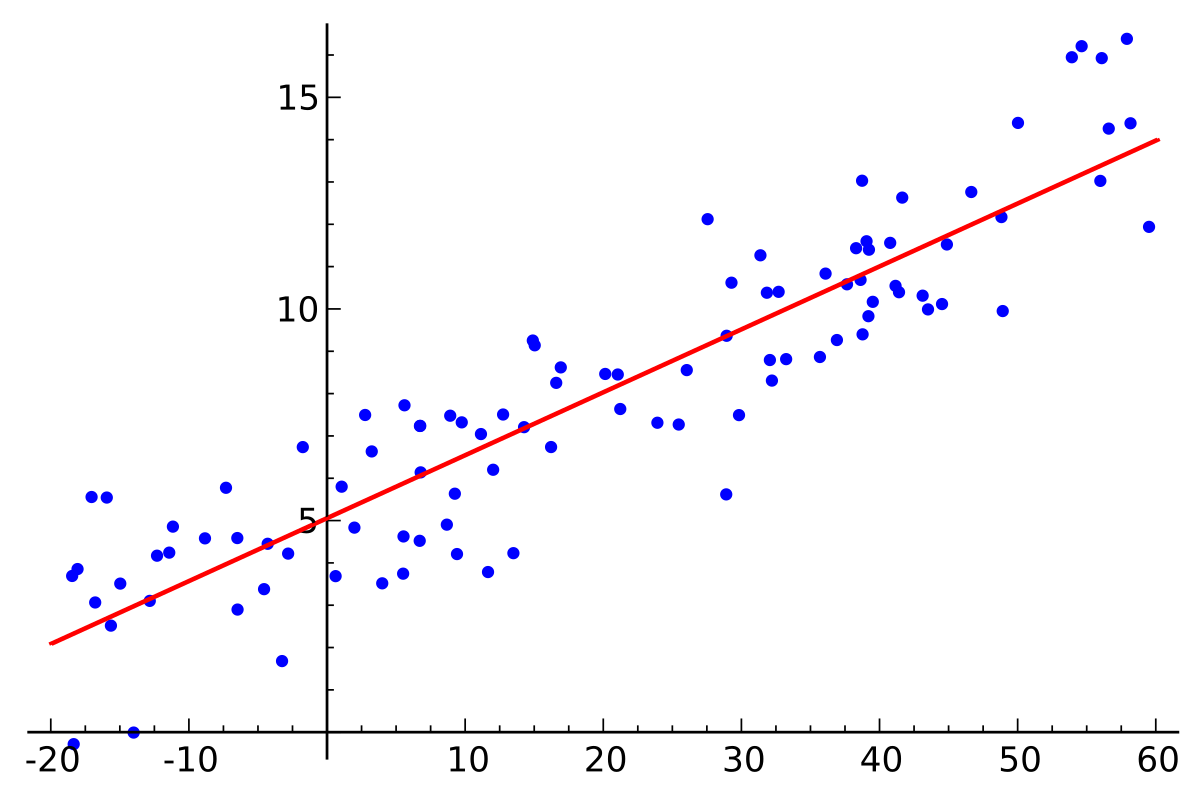
光说理论意义不大，比如：和小冰聊天的过程，她根据你说的话返回一个字符串（一句话），她返回这句话的过程其实就是一个回归的过程。

什么叫分类（classify）？

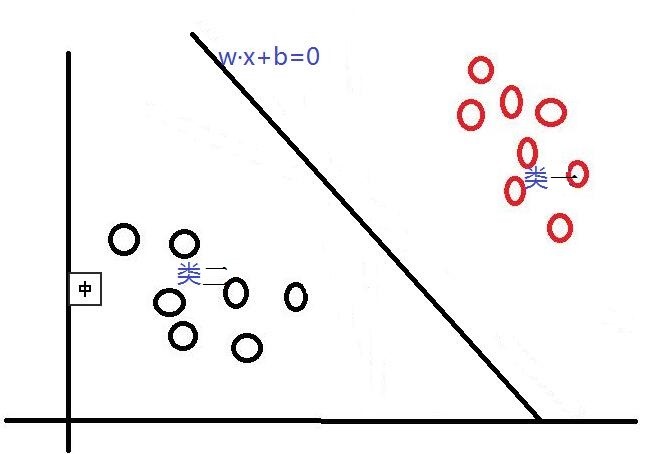
由已知数据（已标注的）通过计算得到一个类别。比如：现在知道小曹182cm，平均每厘米质量为1kg，通过计算得到重量为182kg，这个过程叫回归。根据计算结果我们得出一个结论，小曹是个胖纸，这个过程就属于分类。

这里要特别注意：监督学习常用的“逻辑回归（Logistic Regression）”属于典型的分类方法，而不是回归。

算法模型

接下来一起了解几个监督学习中主要的算法模型：

• K—近邻算法（k-Nearest Neighbor）
• 决策树（Decision Tree）
• 朴素贝叶斯（Naive Bayes）

1. 近邻算法

近邻算法听起来很高大上，但其实思想很简单，让我们先来建立一个模型。

K-近邻算法里的K，是人为设定的一个值，图中的K就是3，那么被框住的三个同学就都算小曹的“邻居”。有句老话说得好啊，人以类聚，物以群分，小曹的体重肯定和周围的人差不多，我们就取三个人的平均值110kg作为小曹的体重，不是邻居的同学们就不考虑了。这是近邻算法的回归模型。

好了，如果是近邻算法的分类模型呢？

应该不用我说了吧，小曹的三个邻居都胖，所以小曹也肯定胖。

这就是K-近邻算法的核心思想，由K确定“近邻”的范围，由近邻的数值和属性得出特定未知变量的数值和属性。

当然了，这个模型是简化之后的，在实际处理的时候，数据的分布都是经过了处理，按一定规则在某个特征空间规律分布的（不是我这样乱画的），只有这样“近邻”才有意义。

特别的，当K值过大的是时候会欠拟合（underfitting），K值过小的时候会过拟合（overfitting）。欠拟合和过拟合在后文解释，想深入了解算法可以在文末查看参考资料。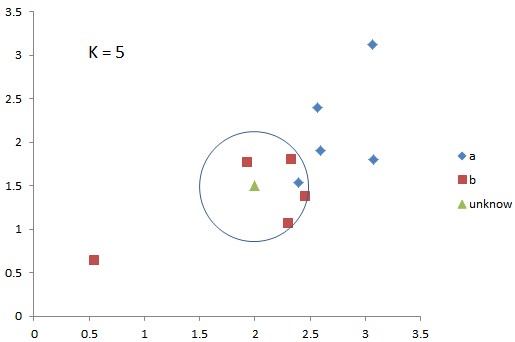

2. 决策树

决策树，就是N个“if”和“then”搭配组成的集合，通过多次决策返回某一特征/类别，以结果的高纯度为目标。决策树只要了解几个名词（熵、信息增益、信息增益率），一个模型（特征选择、生成决策树、剪枝）和三个算法（ID3、C4.5、CART）。

熵的概念大家高中物理课都学过，它的大小代表了一个系统的混乱程度。决策树系统内的熵表示每一条分支结果的纯度，决策树可以说是一个分类的过程，每一类的特征越明显，每一个类别内的数据越相似，熵就越小，纯度就越高。

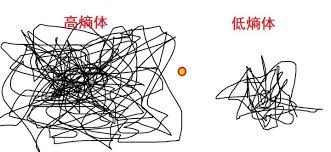
信息增益（用于ID3）是针对节点设定的，节点就是某个属性的分类器，经过这个节点分类后，决策树的熵越小，说明这个节点的信息增益越大。很好理解，我们选择节点肯定要选择能让系统纯度更高的那个。但是问题来了，按照这个规则选取节点的话，总会偏向数量较多的那部分数据。

所以专家们又提出了信息增益比（用于C4.5），用熵减的比率来判断节点的属性，在一定程度上校正了偏向数量较多的问题。

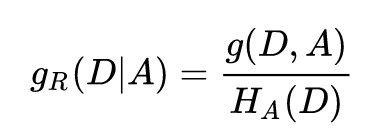
该说人话了，下面举个栗子来说明一下上述三个名词。

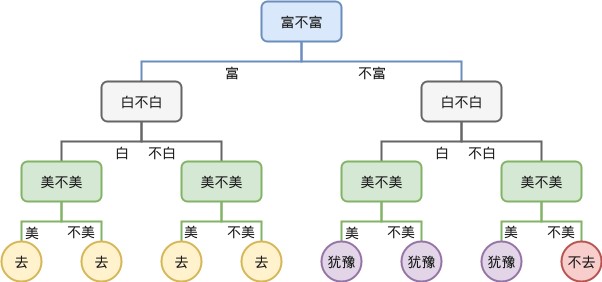
假设我们要通过一个模型来判断一个人是不是RICH。

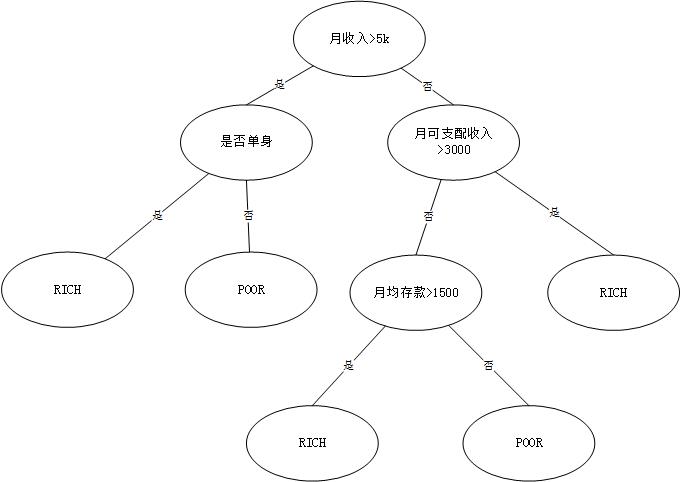
这就是一个简单的二分决策树模型，二分就是指一个节点（判断的圈圈）只分出两个类别，判断yes or not。

熵就是我们判断出来的结果准不准确，从这个模型来看，熵肯定是很大的，因为有很多因素没有加入进来考虑，比如：他是不是有过去的存款，家庭是不是有遗产等等。如果在某个分类下穷人里混进了很多有钱人，就说明它的熵大。基尼系数用于CART(Classification And Regression Tree)，和熵的意义相似。

信息增益简单地说，就是某一个属性的判断，能把多少人分开。比如说：如果设定判断的属性为月可支配收入>3000能让分类到RICH的穷人最少，我们就说它是一个信息增益很大的节点。

原本一个RICH圈圈里有100个穷人，占圈圈里总人数的1%，我们认为分出这个圈圈节点的信息增益很高。这个情况下，使用信息增益和信息增益比的效果，是差不多的。

但如果现在我们不止采用二分法，ID3（用信息增益）算法很可能选择“身份证号”作为判断节点，这样分类出来的每一个小圈圈的熵都将极高（因为一个圈圈只有一个人），但这样的分类是没有意义的（过拟合）。

优化后的C4.5算法（采用信息增益比）就是为了防止这种情况发生，在原来的信息增益基础上除以熵，能够“惩罚”上面发生的情况，让节点的选取更加合理。

到这里我们已经搞清楚了三个名词、两个算法（ID3、C4.5）和一个模型里的两步（特征选择和生成决策树）了。还剩下剪枝和CART算法。

前面的ID3和C4.5都可以对决策树进行多分，但是CART只能进行二分决策树的生成，它可以创建分类树（得到一个类别）和回归树（得到一个值）。

CART算法采用GINI指数来进行特征选择（也就是节点判断属性的确认），GINI指数是度量数据划分的不纯度，是介于0~1之间的数。GINI值越小，表明样本集合的纯净度越高，GINI值越大表明样本集合的类别越杂乱。（和熵相似）

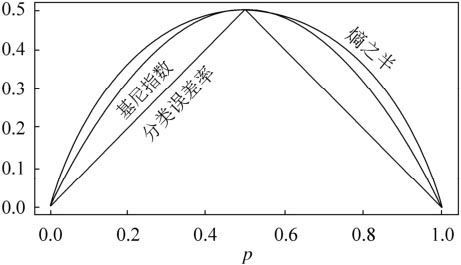
看上面的图，这也可以是CART算法的生成模式。

当我们判断的最终结果不止两个的时候，可能这棵树就会变得很庞大（节点和圈圈都很多），这个时候就需要“剪枝”——去掉多余的节点。

剪枝方法有两种：预剪枝和后剪枝。

• 预剪枝即在决策树生成前，通过一定规则，避免某些节点的生成；
• 后剪枝则是在决策树生成之后进行剪枝。

预剪枝的好处就是省事，但是因为事先确定的规则，可能没有考虑到一些特定且重要的情况下的数据，有可能导致欠拟合。

后剪枝能够让决策树拥有更好的拟合度，但是相对耗费的时间也更多，过程更复杂。

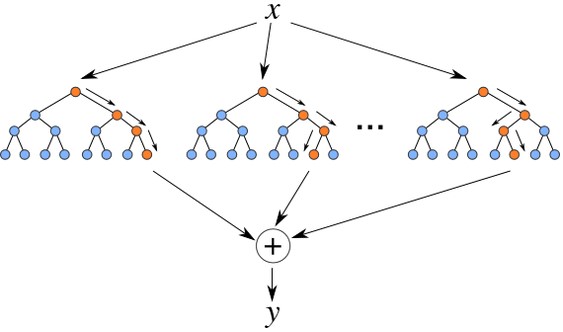
再提一下“随机森林（Random Forest）”。我们知道，三个臭皮匠，顶个诸葛亮。有时候一颗决策树不能对数据做出最准确的分类，这个时候我们通过一定的规则生成很多颗决策树，让所有的决策树处理同一组数据，经过处理之后这样往往能得到更精确的结果。人多力量大，不外如是。

3. 朴素贝叶斯

朴素贝叶斯（Naive Bayes）中的“朴素”，表示所有特征变量间相互独立，不会影响彼此。主要思想就是：如果有一个需要分类的数据，它有一些特征，我们看看这些特征最多地出现在哪些类别中，哪个类别相应特征出现得最多，就把它放到哪个类别里。基本原理还是来自贝叶斯定理。

这样看起来感觉这个方法贼简单，其实真的很简单。（虽然看了我不知道多久才看懂）。

比如说：我们要判断一个长得像胶囊（特征1），通体黄色（特征2），穿着背带裤（特征3），有点智障（特征4）的东西属于什么类别，我们经过遍历（把所有类别和类别包含的所有特征看一遍），发现小黄人（某个类别）出现这些特征的频率很高，那我们得出一个结论，他们是小黄人。

但是朴素贝叶斯方法对特征的划分很敏感，比如说：如果我们没有“长得像胶囊”这一项特征，那它就可能是很多东西了…

最后让我们来用两张图解释一下过拟合和欠拟合。

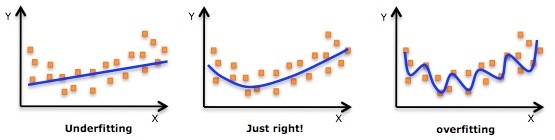
参考文献：

• KNN算法：https://www.cnblogs.com/ybjourney/p/4702562.html
• KNN算法：https://zhuanlan.zhihu.com/p/25994179；https://zhuanlan.zhihu.com/p/26029567，接上一篇，拓展了一些。
• 比较硬的决策树和相应算法介绍：https://www.cnblogs.com/Peyton-Li/p/7717377.html
• 决策树Decision Tree原理与实现技巧：https://blog.csdn.net/xbinworld/article/details/44660339
• C4.5 （信息增益率的含义讲的很清楚，算法实现也较详细）：https://blog.csdn.net/fanbotao1209/article/details/44776039
• 信息熵、条件熵、信息增益、信息增益比、GINI系数：https://blog.csdn.net/bitcarmanlee/article/details/51488204
• 我们为什么需要信息增益比，而不是信息增益？：https://blog.csdn.net/olenet/article/details/46433297
• 信息增益与信息增益比（比较简单）：https://www.jianshu.com/p/268c4095dbdc
• 把CART算法说的很明白：https://blog.csdn.net/u010089444/article/details/53241218
• 维基百科-朴素贝叶斯分类器：https://zh.wikipedia.org/wiki/%E6%9C%B4%E7%B4%A0%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%88%86%E7%B1%BB%E5%99%A8
• 请用简单易懂的语言描述朴素贝叶斯分类器？ – 短发元气girl的回答 – 知乎，很走心的笔记…：https://www.zhihu.com/question/19960417/answer/347544764
• 数学之美番外篇-平凡而又神奇的贝叶斯方法，很长，值得一读：http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/

图片来源：自制、GOOGLE、知乎

作者：小曹，公众号：小曹的AI学习笔记

本文由 @小曹 原创发布于人人都是产品经理。未经许可，禁止转载

题图来自Unsplash，基于CC0协议