优秀的增长黑客，不会去投机取巧“制造数据”，而是认真思考和试验，用科学可信的数据来指导自己和企业的决策，通过无数次失败的和成功的AB测试试验，总结经验教训，变身能力超强的超级英雄。

辛普森悖论（Simpson’s Paradox）是英国统计学家E.H.辛普森（E.H.Simpson）于1951年提出的悖论，即在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。

举一个辛普森悖论的简单小例子：一个大学有商学院和法学院两个学院。这两个学院的女生都抱怨“男生录取率比女生录取率高”，有性别歧视。但是学校做总录取率统计，发现总体来说女生录取率却远远高于男生录取率！

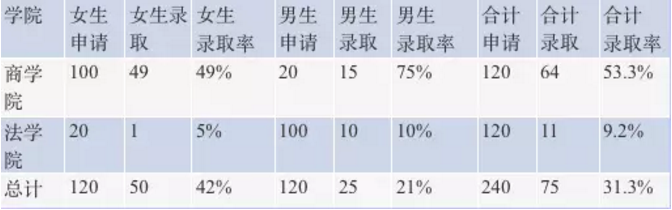
商学院男生录取率75%高于女生录取率49%，法学院男生录取率10%也高于女生录取率5%，但是总计来说男生录取率只有21%，只有女生录取率42%的一半。

为什么两个学院都是男生录取率高于女生录取率，但是加起来男生录取率却不如女生录取率呢？主要是因为这两个学院男女比例很不一样，具体的统计学原理我们后面会详细分析。

这个诡异（Counter intuitive）的现象在现实生活中经常被忽略，毕竟只是一个统计学现象，一般情况下都不会影响我们的行动。但是对于使用科学的 AB 测试进行试验的企业决策者来说，如果不了解辛普森悖论，就可能会错误的设计试验，盲目的解读试验结论，对决策产生不利影响。

我们用一个真实的医学 AB 测试案例来说明这个问题。这是一个肾结石手术疗法的 AB 测试结果：

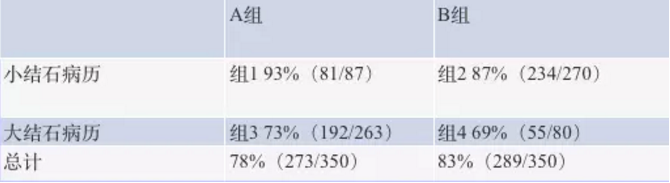
看上去无论是对于大型结石还是小型结石，A 疗法都比 B 疗法的疗效好。但是总计而言，似乎 B 疗法比 A 疗法要好。

这个 AB 测试的结论是有巨大问题的，无论是从细分结果看，还是从总计结果看，都无法真正判断哪个疗法好。

那么，问题出在哪里呢？这个 AB 测试的两个实验组的病历选取有问题，都不具有足够的代表性。参与试验的医生人为的制造了两个试验组本身不相似，因为医生似乎觉得病情较重的患者更适合 A 疗法，病情较轻的患者更适合 B 疗法，所以下意识的在随机分配患者的时候，让 A 组里面大结石病历要多，而 B 组里面小结石病历要多。

更重要的问题是，很有可能影响患者康复率的最重要因素并不是疗法的选择，而是病情的轻重！换句话说，A 疗法之所以看上去不如 B 疗法，主要是因为 A 组病人里重病患者多，并不是因为 A 组病人采用 A 疗法。

所以，这一组不成功的 AB 测试，问题出在试验流量分割的不科学，主要是因为流量分割忽略了一个重要的“隐藏因素”，也就是病情轻重。正确的试验实施方案里，两组试验患者里，重病患者的比例应该保持一致。

因为很多人容易忽略辛普森悖论，以至于有人可以专门利用这个方法来投机取巧。举个例子，比赛100场球赛以总胜率评价好坏。取巧的人专找高手挑战20场而胜1场，另外80场找平手挑战而胜40场，结果胜率41%；认真的人则专挑高手挑战80场而胜8场，而剩下20场平手打个全胜，结果胜率为28%，比41%小很多。但仔细观察挑战对象，后者明显更有实力。

从这几个辛普森悖论的例子出发，联想到我们互联网产品运营的实践里，一个非常常见的误判例子是这样的：拿1%用户跑了一个试验，发现试验版本购买率比对照版本高，就说试验版本更好，我们要发布试验版本。其实，可能只是我们的试验组里圈中了一些爱购买的用户而已。最后发布试验版本，反而可能降低用户体验，甚至可能造成用户留存和营收数额的下降。

那么，如何才能在 AB 测试的设计，实施，以及分析的时候，规避辛普森悖论造成的各种大坑呢？

最重要的一点是，要得到科学可信的 AB 测试试验结果，就必须合理的进行正确的流量分割，保证试验组和对照组里的用户特征是一致的，并且都具有代表性，可以代表总体用户特征。这个问题一直是 AppAdhoc A/B Testing 云服务的云端系统着力研究和解决的问题。

在这里，特别要提出一下这个问题的一个特殊属性：在流量试验越大时，辛普森悖论发生的条件越有可能触发。这是一个和大数定理以及中心极限定理等“常规”实践经验完全不同的统计学现象。换句话说，大流量试验比小流量试验可以消除很多噪音和不确定性，但是反而可能受到辛普森悖论的影响。

举个例子说明：如果只是拿100人做试验，50人一组随机分配，很可能是28男22女对22男28女，每个性别只是相差6个人而已。如果是拿10000人做试验，5000人一组随机分配，很可能是2590男2410女对2410男2590女，每个性别就差了180人，而这180人造成的误差影响就可能很大。

除了流量分配的科学性，我们还要注意 AB 测试的试验设计与实施。

在试验设计上，如果我们觉得某两个变量对试验结果都有影响，那我们就应该把这两个变量放在同一层进行互斥试验，不要让一个变量的试验动态影响另一个变量的检验。如果我们觉得一个试验可能会对新老客户产生完全不同的影响，那么就应该对新客户和老客户分别展开定向试验，观察结论。

在试验实施上，对试验结果我们要积极的进行多维度的细分分析，除了总体对比，也看一看对细分受众群体的试验结果，不要以偏盖全，也不要以全盖偏。一个试验版本提升了总体活跃度，但是可能降低了年轻用户的活跃度，那么这个试验版本是不是更好呢？一个试验版本提升总营收0.1%，似乎不起眼，但是可能上海地区的年轻女性 iPhone 用户的购买率提升了20%，这个试验经验就很有价值了。

分层试验，交叉试验，定向试验是我们规避辛普森悖论的有力工具。

规避辛普森悖论，还要注意流量动态调整变化的时候新旧试验参与者的数据问题，试验组和对照组用户数量的差异问题，以及其他各种问题。而优秀的增长黑客，不会去投机取巧“制造数据”，而是认真思考和试验，用科学可信的数据来指导自己和企业的决策，通过无数次失败的和成功的AB测试试验，总结经验教训，变身能力超强的超级英雄。

作者：王晔，吆喝科技创始人兼 CEO

本文由 @王晔 原创发布于人人都是产品经理。未经许可，禁止转载。