希望通过我们的几篇文章，能够帮助你更好的了解A/B测试和置信区间，一起实现用A/B测试驱动产品优化。

A/B测试的实质是对照试验，即通过对几个不同的版本进行对比，从而选出最优版本。在这个过程中，需要分析处理在试验中收集到的数据，并应用统计学上的方法对数据进行验证，看它是否符合我们最初的设计目标，或分析它的结果效应如何。这一章我们就将跟大家谈谈这种方法——假设检验。

假设检验的定义

假设检验是先对总体的参数提出某种假设（比如说转化率的平均值），然后利用样本数据判断假设是否成立的过程。在逻辑上，假设检验采用了反证法，即先提出假设，再通过适当的统计学方法来计算这个假设可能性的大小。

由于统计得出的结果来自于随机样本的数据，结论不可能为绝对的，所以我们只能根据概率上的一些依据进行相关的判断。这里依据的是小概率思想（即显著性水平 p<0.05的小概率事件在一次试验中基本上不会发生），也就是说当原假设的可能性小于认定的某一标准的话，则拒绝原假设（认为这个假设是不成立的），反之则接受原假设。

具体到A/B测试里的假设检验，就是指假设试验版本的总体参数（优化指标均值）等于对照版本的总体参数，然后利用这两个版本的样本数据来判断这个假设是否成立。

如果样本数据拒绝原假设，我们说检验的结果是显著的；反之，我们则说结果是不显著的。一项检验在统计上是“显著的”，意思是指这样的样本数据不是偶然得到的，即不是抽样的随机波动造成的，而是由内在的影响因素导致的。

假设检验的基本概念

为了更好地理解假设检验，我们在下面列出了一些与之有关的基本概念。

• 统计假设：是对总体参数(包括总体均值μ等)的具体数值所作的陈述。
• 原假设：是试验者想收集证据予以反对的假设，又称“零假设”，记为H0；对比试验中的原假设就是试验版本的总体均值等于对照版本的总体均值。
• 备择假设：也称“研究假设”，是试验者想收集证据予以支持的假设，记为H1；对比试验中的备择假设就是试验版本的总体均值不等于对照版本的总体均值。
• 双侧检验与单侧检验：如果备择假设没有特定的方向性，并含有符号“≠”，这样的称为双侧检验。如果备择假设具有特定的方向性，并含有符号“>”或“<”的假设检验，称为单侧检验。

原假设和备择假设是一个完备事件组，而且相互对立。在一项假设检验中，原假设和备择假设必有一个成立，而且只有一个成立。在对比试验中，因为我们试验的目的是通过反证法证明试验版本和对照版本有明显的不同（提升），所以我们的原假设是试验版本的总体均值等于对照版本的总体均值。

假设检验的两类错误

假设检验中有两类错误，需要我们在试验过程中加以避免。

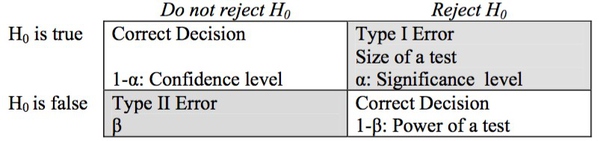
• 第 I 类错误（弃真错误）：原假设为真时拒绝原假设；第 I 类错误的概率记为 α(alpha)。
• 第 II 类错误（取伪错误）：原假设为假时未拒绝原假设。第 II 类错误的概率记为 β(Beta)。

其中，α 是一个概率值，表示原假设为真时, 拒绝原假设的概率，也称为抽样分布的拒绝域。在这两类错误中，相对更加严重的是第 I 类错误，为了尽量避免第一类错误的发生，α 的取值应尽可能小。α 值由试验者事先确定，常见的有 0.01，0.05和0.10 。对比试验中使用的 α 值是 0.05(5%)，这是显著性检验中最常用的小概率标准值。

假设检验的决策标准

因为假设检验主要是通过观察样本结果，再计算总体假设的可能性，最后判断出假设的正确与否。那么可能性的标准是什么呢？需要根据显著性水平 P-Value 进行计算。

在这里简要说明一下显著性水平 p（p-value），是指在原假设为真的条件下，样本数据拒绝原假设这样一个事件发生的概率。例如，我们根据某次假设检验的样本数据计算得出显著性水平p=0.04；这个值意味着如果原假设为真，我们通过抽样得到这样一个样本数据的可能性只有 4%。

那么，0.04 这个概率或者说显著性水平到底是大还是小，够不够用来拒绝原假设呢？这就需要把 p 和我们采用的第 I 类错误的小概率标准 α 来比较确定。假设检验的决策规则：

若 p ≤ α，那么拒绝原假设；

若 p > α，那么不能拒绝原假设。

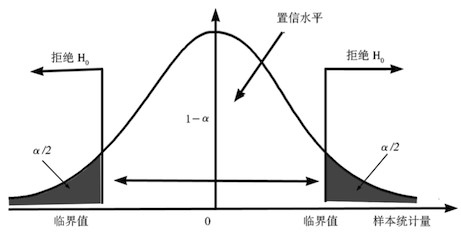
如果 α 取 0.05 而 p = 0.04，说明如果原假设为真，则此次试验发生了小概率事件。根据小概率事件不会发生的判断依据，我们可以反证认为原假设不成立。

显著性水平 p 的计算公式取决于假设检验的具体方式，在这里就不具体展开了。

关于假设检验的基础知识就介绍到这里，在之后的内容中，我们将分别对显著性水平的P-Value、T检验等进行详细的介绍。

作者：吆喝科技，微信公众号（appadhoc）。

本文由 @吆喝科技 原创发布于人人都是产品经理。未经许可，禁止转载。