100种分析思维模型之:大数定理
本文将带你深入了解大数定理的概念和应用,通过实际案例展示如何利用这一统计学原理来提高我们对随机事件的理解和预测能力,希望对你有所帮助。

你好,我是林骥。在我们的日常工作、生活和学习中,经常会面对着各种不确定性的随机事件,此时我们不妨运用统计思维,发现事物背后的规律。
在统计思维的背后,还有一把神奇的钥匙,那就是大数定理。
下面介绍 100 种分析思维模型的第 73 种:大数定理,它能帮助我们更好地理解规律背后的原理,提升预测未来的能力。
一、为什么学习大数定理?
对于很多人来说,感觉数学很难,不知道学数学有什么用,更不知道怎么用。因此,只停留较低的水平,无法跟日常运用对接起来,结果白白浪费了很多时间和精力。
事实上,在我们的日常生活中,每天都可以用到数学,从简单的加减乘除,到一些复杂的公式定理,只要运用得当,就能发挥出巨大的价值。
我们每天都在面临各种各样的风险,出门有风险,不出门也有风险;吃饭有风险,不吃饭也有风险;坐车有风险,坐飞机也有风险……
风险几乎无处不在,但有些风险是可控的,有些风险是不可控的;有些风险是可预知的,有些风险是不可预知的;有些风险是比较大的,有些风险是比较小的……
其实,我们完全不必「杞人忧天」,只要学会灵活运用大数定理,就可以更合理地评估风险大小,进而做出正确的决策。
如果没有大数定理的话,那么所有的随机实验,以及一切通过统计数据发现事物背后的规律,都将变得没有什么意义。
正是因为有了大数定理,我们才可以通过现实观察到的数据,去预测未知的事物,并且因此有了科学理论的支撑。
总之,通过学习大数定理,可以帮助我们正确地理解和分析数据,预测随机事件发生的规律,避免被事物的表象所误导,提高数据分析和科学决策的能力,进而提升我们的认知水平。
二、什么是大数定理?
大数定理是概率论与数理统计中的一个基本定理,它的核心思想是:
如果进行多次随机试验,只要样本数量越多,它们的平均值就越趋近于数学期望值。
比如,在抛硬币的试验中,正常情况下出现正面的概率是 50%,按照大数定理,抛硬币的次数越多,出现正面的次数就越趋近于总次数的 50%。假如你抛 10 次硬币,出现了 8 次正面,这并不能说明硬币有问题,或者说大数定理有问题,也许是因为你抛的次数还不够多。当你抛的次数足够多之后,正常情况下都会回归均值的。
下面我用 Python 代码模拟了抛硬币的过程:
import numpy as np
import scipy.stats as st
import matplotlib as mpl
import matplotlib.pyplot as plt# 防止中文乱码
mpl.rcParams[‘font.sans-serif’]=[u’simHei’]
mpl.rcParams[‘axes.unicode_minus’]=False# 定义次数和范围
n = 1000
x = np.arange(1, n+1, 1)
# 定义数组:出现正面的比例
y = []
# 循环计算
for i in x:
data = st.bernoulli.rvs(size=i, p=0.5) # 伯努利分布数据
y.append(sum(data)/len(data)) # 追加出现正面的比例# 设置图表的大小
plt.figure(figsize=(18.8, 8))# 作图设置
plt.xlabel(‘抛硬币次数’, fontsize=20)
plt.ylabel(‘出现正面的比例’, fontsize=20)
plt.tick_params(axis=’both’, which=’major’, labelsize=16)# 作图并展示
plt.plot(x,y)
plt.plot([n,0.5], [0.5,0.5], ‘r’) # 均值参考线
plt.show()
运行结果如下:
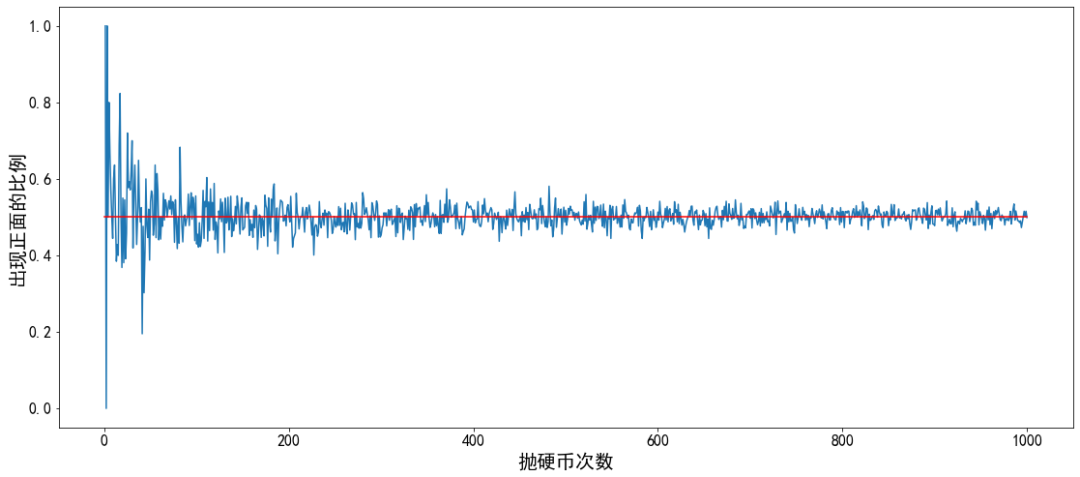
从图中可以直观地看出,随着抛硬币次数的增加,出现正面的比例越来越趋近于 0.5。
大数定理有多种不同的形式,包括伯努利大数定理、切比雪夫大数定理、辛钦大数定理、波莱尔大数定理、柯尔莫哥洛夫大数定理等。
不同的大数定理,在前提假设方面略有差异,在结论的深度和角度等方面也有所不同,但它们都经过数学家的严格证明,否则就只能叫「大数定律」。
严格来说,定理与定律是有区别的。
定理是经过逻辑推理或严格证明的原理,不允许有例外情况。比如平面几何中的勾股定理,无论直角三角形怎么变,两条直角边的平方和,一定等于斜边的平方。
定律是通过观察或实验获得的经验规律,在一定条件下可能会失效。比如牛顿的经典力学三大定律,在微观环境下可能不成立。
尽管定理与定律的概念略有不同,但是由于在「大数定理」被数学家严格证明之前,人们已经习惯称之为「大数定律」。所以,现在人们所说的「大数定律」,通常就是指「大数定理」。
三、怎么运用大数定理?
无论是在工作中,还是在生活中,大数定理都为我们提供了一种应对不确定性的方法。
我们可以把运用大数定理,去发现一些事物背后的规律,从而帮助我们做出正确的判断和决策。
比如,通过量化自己的时间价值,假设你每小时的价值是 1000 元,现在有一件事情,需要你花 1 个小时,有 20% 的可能性获得 8000 元的收益,另外有 80% 的可能性收益为 0 元,那么这件事是否值得去做呢?
答案是肯定的,因为做这件事的数学期望是 20%*8000=1600 元,明显高于你的时间价值。虽然有 80% 的可能性浪费一个小时的时间,但是按照大数定理,长期来看,这样的事情做得越多,就越有可能获得更多的收益。
运用大数定理,核心不在于梳理已知的事实,而在于推断未知的可能性。
在推断未知的过程中,你可能需要用到贝叶斯思维,就是从过去已知条件出发,去推测未来事件发生的概率。
这有点像福尔摩斯探案的过程,当他发现在凶手作案的时间里,平常见人就叫的狗却没有叫,因此推断出肯定是熟人作案。
运用大数定理,当一件大概率应该发生的事情没有发生时,其中肯定存在某种原因,你在经过分析和排查之后,也许就能揭示其中的真相。
四、最后的话
数据的应用离不开统计学,而大数定理是统计学的基石,它保障了概率思维和统计思维的科学性和实用性,让我们能够更好地认识世界的规律,进而做出更加合理的决策。
有些人喜欢认真做好每一件小事,虽然短期来看收益比较小,但是大概率能够成功,经过时间的日积月累,就有可能形成复利效应。
另外有些人则喜欢潜心做一件大事,虽然成功率比较低,但是一旦成功,收益非常高。
无论你选择做哪种人,只要符合大数定理,最终都有可能获得自己想要的结果。
然而,有些人却违背大数定理去做事。比如,想要靠赌博发家致富,这几乎是不可能的,因为赌场早已算准了赌徒输钱的概率。
一个人的认知,决定了一个行为。如果我们学会运用大数定理,也许就不会去做赌博和盲目投资之类的傻事了。
人只能赚到自己认知范围之内的钱,凭运气赢得的财富,最后都会凭实力输回去。
只有努力提升自己的认知水平,从过去收集数据,到现在分析思考,再到未来指导行动,做好风险的管控,才能让生活变得更加幸福。
公众号:林骥,《数据化分析》作者
本文由 @林骥 原创发布于人人都是产品经理。未经作者许可,禁止转载。
题图来自Unsplash,基于CC0协议。
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务。
- 目前还没评论,等你发挥!


 起点课堂会员权益
起点课堂会员权益






