100种分析思维模型之:中心极限定理
本文将带你探索中心极限定理的奥秘,了解它如何帮助我们从随机事件中发现规律,并应用于日常生活和决策中,希望对你有所帮助。
你好,我是林骥。
在我们的日常生活中,一些看似没有规律的随机事件,其实背后隐藏着一个神奇的定理。
下面介绍 100 种分析思维模型的第 74 种:中心极限定理,它能帮助我们更好地理解事物背后的规律。
一、为什么学习中心极限定理?
学习中心极限定理有很多好处,下面简要总结 3 点:
① 更好地理解数据分布
通过学习中心极限定理,我们可以更好地理解数据分布的特点,从而更准确地提取有价值的信息。
② 增强数据分析的能力
学习中心极限定理可以帮助我们更好地分析数据,提升我们的数据分析能力,因为它不仅是一种理论工具,更是一种思维方式。
③ 更好地解决实际问题
中心极限定理有着广泛的应用,比如市场调研、质量控制、风险评估、医学研究、社会调查等,掌握中心极限定理,能帮我们更好地解决现实生活中遇到的问题。
总之,中心极限定理为我们提供了一种强有力的工具,帮助我们更好地理解现实世界,进而给我们带来深远而有益的影响。
二、什么是中心极限定理?
中心极限定理是概率论与数理统计中的重要定理,它的核心思想是:无论原始随机变量如何分布,当样本量足够大时(至少 30 个),样本均值总会趋近于正态分布。
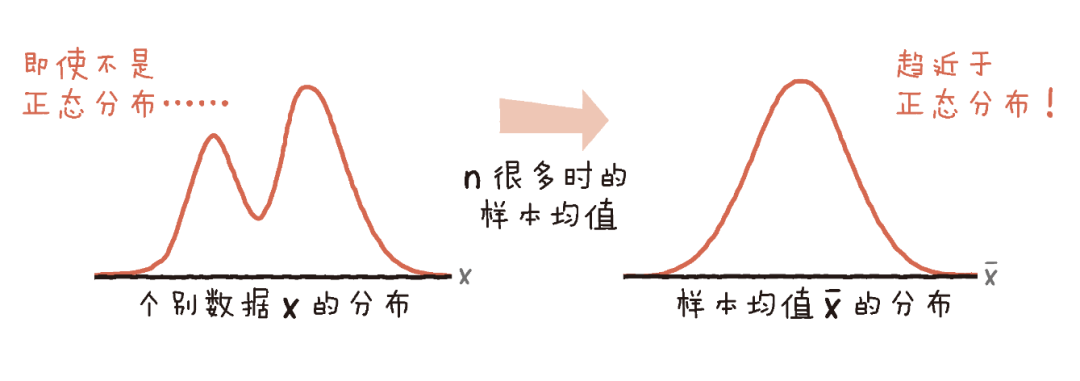
比如,虽然总体上人们的财富属于幂律分布(符合二八法则),但是如果每次随机抽取 n 个人,总共随机抽 m 次,那么这 m 次抽样的平均值就趋近于正态分布。
需要注意的是,样本量 n 不能太小,且为了保障抽样的随机性,每次抽样都要保持独立,不能相互影响。
如下图所示,随着样本量 n 的增加,无论总体分布的形状如何变化,最终样本均值都将趋近于正态分布。
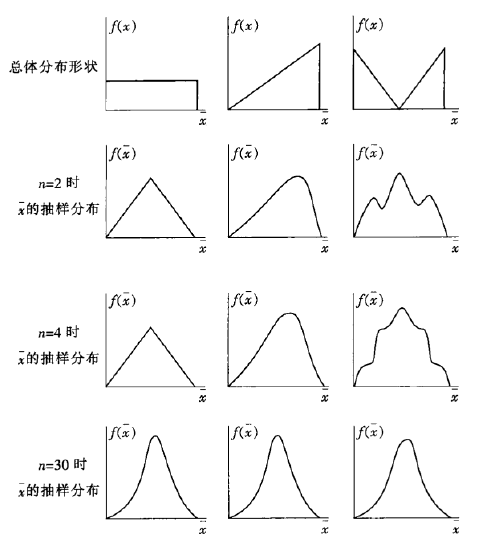
按照中心极限定理揭示出来的规律,每个随机事件最终都将演化成正态分布的样子。
也就是说:所有的分布,不是正态分布,就是在变成正态分布的路上。
这个过程类似于熵增定律:宇宙中一切封闭的系统,在没有外力做功的情况下,都在朝着熵增(混乱、无序)的方向发展。
三、怎么运用中心极限定理?
运用中心极限定理,我们可以解释现实生活中的很多现象。
比如,为什么人类的身高服从正态分布?
这是因为影响一个人身高的因素有很多,有研究表明,除了外在环境的影响之外,人体内至少有 180 个基因会影响人的身高,这些因素可以近似地看作是独立的随机变量。
根据中心极限定理,如果一个事物受到多个独立因素的影响,不管每个因素本身属于什么分布,它们汇总在一起之后,其结果的平均值就会服从正态分布。
我们还可以从中心极限定理中获得启发,用来促进个人的成长。
① 接纳变化
我们不妨把不同的人生经历看作是独立的随机变量,中心极限定理表明,大量随机变量的总和将趋近于正态分布,这意味着无论生活如何变化,虽然中间会有起起伏伏,但是长期来看,大概率都将回归到正常的状态。
在个人成长的过程中,你可能会遇到各种挫折和失败,但你可以从中学到经验和教训,并且随着时间的推移,这些失败的经历将会促进你的成长。
学会接纳世界的不确定性,勇于尝试新的事物,主动适应新的变化,这样就能增加自己的人生体验。
② 持续积累
中心极限定理需要样本量足够大才会生效,个人也需要时间去积累才会成长。你流过的每一滴汗,读过的每一本书,都将随着时间的积累,逐渐改变你的身体,提升你的认知。
当我们养成记录时间和情绪的习惯之后,通过跟踪分析自己的成长数据,就能从中获得一些有价值的信息,从而更加合理地安排好自己的时间,驾驭好自己的情绪,进而加速个人成长。
通过持续努力学习,我们可以不断积累丰富的知识技能,最终实现个人成长的目标。
③ 保持平衡
在中心极限定理中,正态分布是一种均衡的结果。
同理,在个人成长中,保持身心的平衡非常重要。
我们要多关注自己的健康、情绪和人际关系,让自己在不同方面取得均衡的发展,进而过上更加幸福的生活。
总的来说,运用中心极限定理的理念,通过接纳变化、持续积累和保持平衡,我们可以实现更好地成长。
四、最后的话
我们每天都会遇到各种各样的随机事件,如果我们任由其发展,那么生活可能就会变得越来越混乱,逐渐脱离我们的掌控。
比如,睡眠不规律、饮食不规律、情绪不稳定、习惯不好、琐事缠身、浑浑噩噩、得过且过,等等。
要想改变自己的命运,就要学会建立一套开放的系统,相信系统的力量,并选择主动进行管理,坚持长期主义,把无序变成有序,这是一个「逆熵增」的过程。
中心极限定理不仅从理论上证明了正态分布的产生方式,还从根源上揭示了正态分布普遍存在的原因。
也就是说,中心极限定理是「因」,正态分布是「果」。正是因为有了中心极限定理,所以才有正态分布的普遍存在。
普通人改变结果,优秀的人改变原因,而卓越的人改变思维模型。
如果把正态分布比作喜马拉雅山脉,那么中心极限定理就像是青藏高原。正是因为有了青藏高原这个坚实的基础,所以喜马拉雅山脉才能成为世界最高的山脉。
由于中心极限定理如此重要,所以它和大数定理一起,被称为概率论的两大「黄金定理」,为统计学提供了严格的数学证明,打下了坚实的理论基础。
让我们学习并应用中心极限定理,建立一套判断和选择的标准,把局部的随机性,转化为整体的确定性,在数据的汪洋大海中,更加准确地找到前进的方向,最终抵达目的地。
公众号:林骥,《数据化分析》作者
本文由 @林骥 原创发布于人人都是产品经理。未经作者许可,禁止转载。
题图来自Unsplash,基于CC0协议。
该文观点仅代表作者本人,人人都是产品经理平台仅提供信息存储空间服务。
- 目前还没评论,等你发挥!


 起点课堂会员权益
起点课堂会员权益






