企业对于业务指标的监控变得尤为重要。面对日常运营中指标波动的挑战，如何有效识别异常波动，既避免漏报也减少错报，是每个数据驱动型企业需解决的问题。本文提出了一种集成监控方案，结合阈值、3sigma和时间序列方法，以app日活指标为例，展示了如何实现对业务指标的精准监控和异常预警。

一、应用场景

在日常工作中，我们经常面临指标波动的挑战。比如，当DAU指标环比下降10%，我们是否应该触发监控机制呢？为了有效地识别指标异常，我们需要解决两个核心问题：

1. 避免漏报，即确保能够准确地识别异常波动，从而最小化对业务的影响；
2. 减少错报，即避免错误预警，减少不必要的排查工作，以节约人力资源。

本文将介绍一种集成监控方案，能更有效地识别业务指标中的异常情况。

二、解决方案

以app日活指标为例，设计基于阈值、3sigma、时间序列于一体的集成监控方案。

介绍如何实现对日活进行监控，识别指标异常。

1. 基于阈值的监控方案

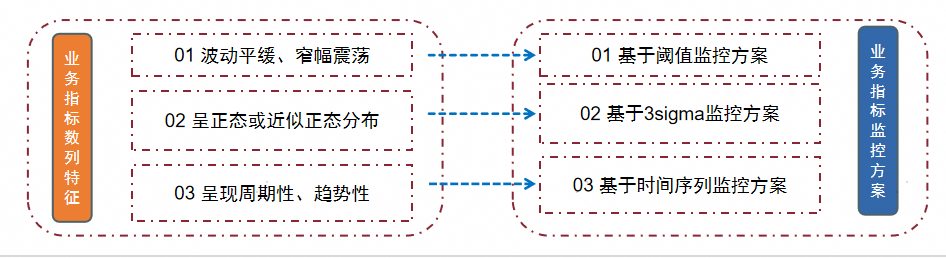
基于阈值的监控方案，主要依赖个人经验设置指标阈值。通常适用于振幅相对平缓的业务数据指标，通常采用的方式有：

• 基于历史数据观测值设置监控阈值，将异常上限设置在历史数据正常值最高点附近，下限设定在最低点附近，一旦业务指标超过设置的上限、下限值触发监控；
• 基于同环比设置监控阈值，基于历史数据同环比波动范围，将阈值设置在同环比历史数据峰值、谷峰附近，当业务指标超过设定值触发监控。

2. 基于3sigma监控方案

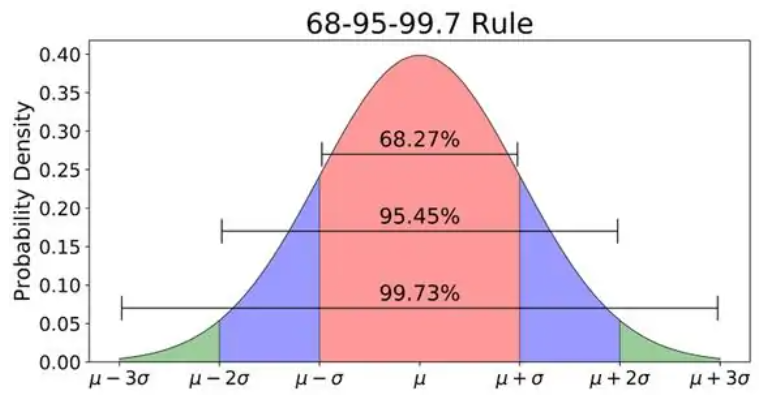
3sigma准则通常适用于对正态或近似正态分布的业务数据，若数据服从正态分布，对数据指标进行计算处理得到标准偏差，按与平均值的偏差在三倍标准差范围内来确定数据分布区间，区间外的指标值则判定为异常值。

即业务指标在满足正态分布的前提下，距离指标平均值3倍标准差之外的值出现的概率很小(P(|x−μ|>3σ)≤0.003)，若在区间外则可认为是异常值。

若数据不服从正态分布，也可以用距离平均值多少倍标准差来描述，但sigma系数需要根据业务数据分布情况来判定。

3. 基于时间序列的监控方案

前文提到数列呈现平稳波动或者服从正态分布的情况，在实际生产过程中，业务指标往往会表现出周期性、趋势性规划。

前两种监控方案往往会出现错报现象，比如在电商节、节假日、周年庆等时期，数据波动较大，前面基于阈值以及3sigma原则的监控往往会误报、触发监控导致不必要排查上的人力投入。

基于时间序列监控方案考虑到业务指标季节性和周期性变化对具体时间点的影响，从业务数据指标历史时间序列中找出变量变化的特征，利用统计学方式预测变量未来趋势以及发展规律，从而测算出预测值。

通过预测值与真实值的偏差程度来识别是否是异常，通常会使用平均绝对百分比误差(MAPE)指标来衡量，如MAPE超出所给的设定值，则判断为异常，从而触发异常监控。以日活指标(t-1)为例。

通过t-2前的历史数据构建预测模型，来预测t-1天的日活值，当业务数据集在t-1天更新指标值(真实值)。

通过计算预测值与真实值之间的平均绝对百分误差来度量偏差程度，依据模型训练精度设定阈值。当触发该阈值时，触发监控进行异常预警。

综上所述，集成监控根据业务指标数列特征构建相应的监控模型来进行异常的识别与预警，整体解决方案如下图：

三、应用案例

以下是以app日活为例，将基于阈值、3sigma、时间序列于一体的监控方案运用在其指标异常监控上。

为举例方便，我们采用2022年10月到12月期间3个月业务数据样本。

1. 基于阈值的监控方案

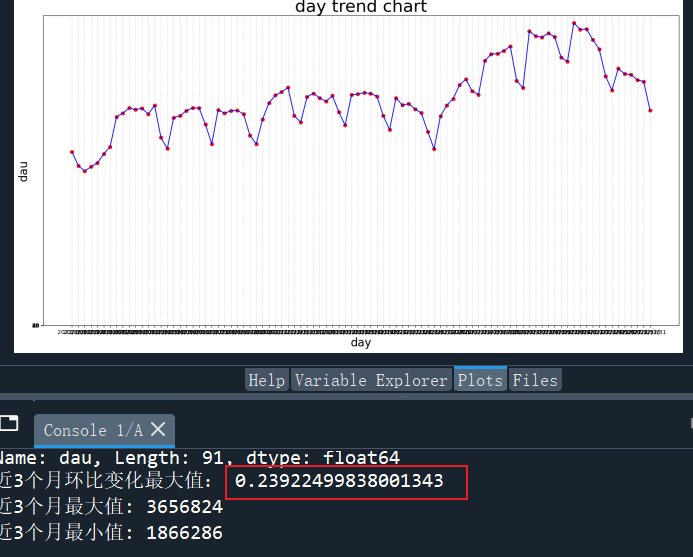
通过计算样本环比最大波动值为23.9%（见下图），可以将阈值设置为该值，当日活环比值超过阈值，如25%超过阈值(23.9%)时，则触发异常监控。

该方案也可以根据样本最大值、最小值来进行阈值监控，当业务指标超过最大、最小值范围时触发监控。

2. 基于3sigma的监控方案

基于上文提到的3sigma准则，我们计算出近3个月的均值、标准差值，在数据呈现近似正态分布情况下，业务指标数据落在数值分布在（μ-3σ,μ+3σ)中的概率约为99.7%，若指标数据落在该区间外，我们则判定为异常值，从而触发监控。

展示效果如下：

3. 基于时间序列的监控方案

进行时间序列预测前，先可以将指标拆分成4部分：

(a)趋势性；(b)季节性；(c) 周期性；(d)随机噪声。

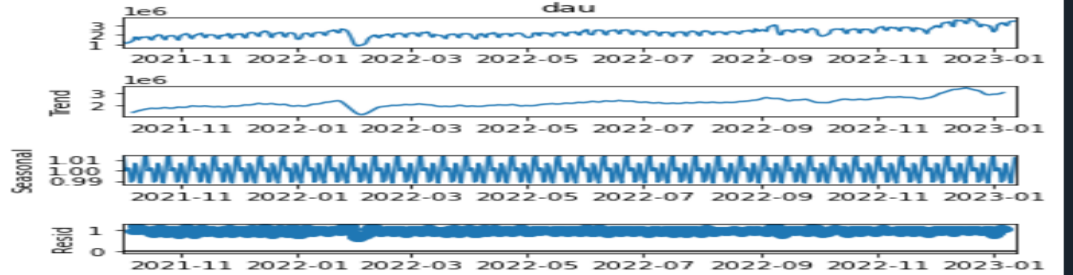
通过观察分解图，来初步识别业务数据指标序列是否平稳。

如果数据是平稳的，可以使用传统的自回归平均移动模型（ARMA）；如果数据是不平稳的，可以使用差分移动自回归平均移动模型（ARIMA）。

在实际应用中，我们会发现传统模型的预测精度效果相对较差，这里我们采用SVR模型来进行预测，对于SVR模型，最主要的参数就是C(惩罚系数)和gamma（核函数自带参数）。

对于C和gamma参数的确定可以通过交叉验证的方法来进行确定，本文采取的是粒子群算法，通过粒子群算法初始化随机解，根据迭代找到最优解。

模型效果如下：

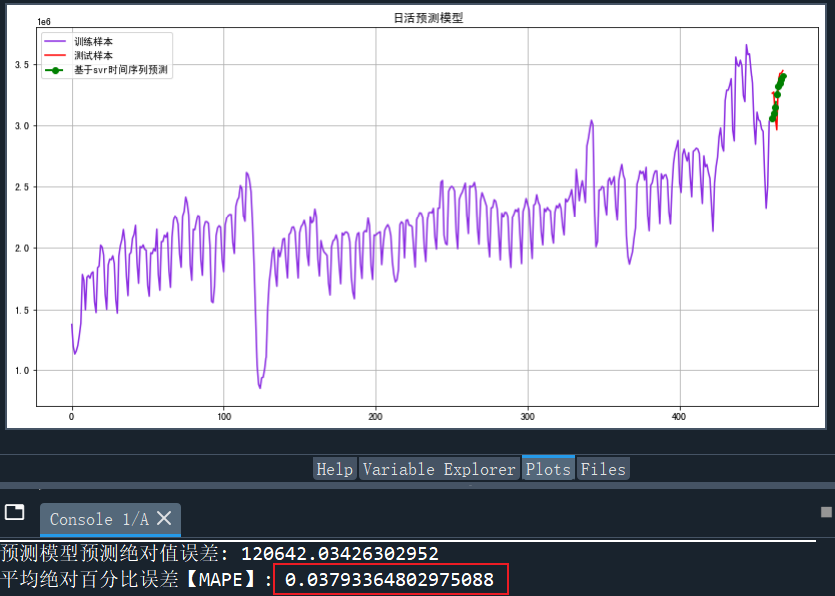
我们可以将真实值与预测值的误差上限设定为6%，这个设定通常会略高于平均绝对百分比误差值（MAPE）的数值（如上图3.79%）。

当误差超过6%的阈值时，将会触发异常监控，及时发现并处理异常情况。

这样可以确保我们对预测值的准确性进行有效监控和控制。

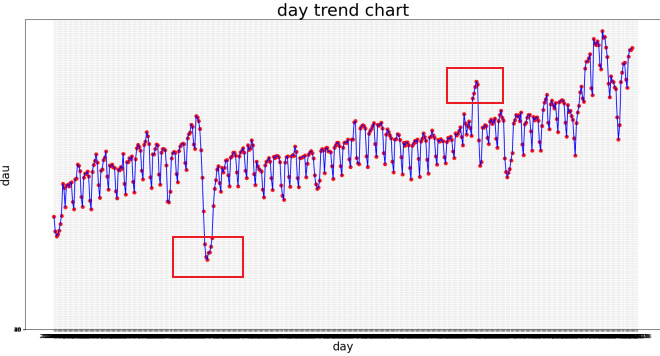
以2023年1.1-2.28期间日活数据为例，监控体系各方案效果，如下：

在日活数据监控中，考虑日活指标的周期性、趋势性采用时间序列模型较合适，从上图的监控效果中，基于时间序列的监控方案效果也是3种方案中最好的，在业务预警中，我们可根据业务数据本身的规律来选取最合适的监控方案。