传统的互联网产品都已经有很成熟的评估指标进行分析，但面对大模型此类新产品，我们如何评价一款产品的好坏？这篇文章，我们就来补充一下这些评估指标的基础知识。

一、常用的模型评估指标类型

在评估模型时，我们一般会用到模型的性能指标、模型的稳定性指标、业务相关指标。另外根据模型应用的不同场景，我们可能还会用到可解释性指标、时效性指标、公平性指标、资源利用指标、鲁棒性指标等。本文将重点介绍模型的性能指标、模型的稳定性指标，其它类型指标感兴趣的可自行深入了解。

1. 性能指标

对于分类问题 ，常用的模型评估性能指标：准确率（Accuracy）、精确率（Precision）、召回率（Recall）、F1 值、AUC值、KS值。

对于回归问题，常用的模型评估性能指标：均方误差（Mean Squared Error，MSE）、均方根误差（Root Mean Squared Error，RMSE）、MAE（平均绝对误差）、R² 系数。

2. 稳定性指标

模型的稳定性是指模型在不同的数据集（如训练集、验证集、测试集）、不同的环境条件（如不同的硬件、软件平台）或者随着时间的推移，其性能表现保持相对一致的特性。常用的稳定性指标有PSI指标。

3. 业务指标

业务指标根据模型解决不同的业务问题而不同，比如在人工智能客服中，常用到的业务指标有智能客服的独立接待率（没有转人工情况下）。

4. 可解释性指标

衡量模型的可解释程度，即能够让用户理解模型是如何做出决策的能力。例如，在一些对决策过程透明度要求较高的领域，如医疗诊断、金融风险评估等，模型的可解释性至关重要。常用的可解释性指标有特征重要性、部分依赖图等。

5. 时效性指标

评估模型的响应速度和更新频率是否满足实际应用的时间要求。在一些实时监控、在线交易等场景中，模型需要快速做出反应并且及时更新以适应数据的变化。常用的指标如推理时间（指模型从输入数据到输出预测结果所花费的时间）。

6. 公平性指标

用于评估模型在不同群体（如不同性别、种族、年龄等）之间是否存在偏差。确保模型不会对某些群体产生不公平的对待，尤其是在涉及到招聘、司法、信贷分配等敏感领域。常用的指标如统计均等差异（计算不同群体（如男性和女性）获得正类预测结果的概率差异）。

7. 资源利用指标

考虑模型在运行过程中对硬件资源（如 CPU、GPU、内存等）的消耗情况。在大规模部署模型或者资源受限的环境中，资源利用效率是一个重要的评估因素。常见的指标如内存占用。

8. 鲁棒性指标

鲁棒性是指模型在面对数据的微小扰动、噪声干扰、对抗攻击或者分布变化等异常情况时，仍然能够保持良好性能的能力。一个鲁棒性强的模型在各种复杂和不确定的实际应用场景中更可靠。常用的指标如对抗攻击的鲁棒性、数据噪声下的鲁棒性。

二、模型评估指标的用法、应用场景、优缺点

1. 准确率（Accuracy）

a. 用法

• 准确率是分类问题中最常用的指标之一，它表示被正确分类的样本数占总样本数的比例。
• 计算公式为：准确率 = （正确分类的样本数 / 总样本数）× 100%。

b. 合理值区间

准确率的取值范围在 0% 到 100% 之间。通常来说，准确率越高越好，但具体的合理值取决于问题的难度和应用场景。

c. 应用场景

适用于各类分类问题，尤其是在类别分布比较均衡的情况下。例如，在识别手写数字的任务中，可以使用准确率来评估模型的性能。

d. 优缺点

• 优点：直观易懂，计算简单。
• 缺点：在类别不平衡的情况下，准确率可能会产生误导。例如，如果一个数据集中 99% 的样本属于一个类别，那么一个总是预测这个多数类别的模型也能获得 99% 的准确率，但实际上这个模型可能没有任何实际价值。

2. 精确率（Precision）和召回率（Recall）

a. 用法

• 精确率也称为查准率，它表示在所有被预测为正类的样本中，真正的正类样本所占的比例。
• 召回率也称为查全率，它表示在所有实际的正类样本中，被正确预测为正类的样本所占的比例。计算公式为：精确率 = 预测中真正的正类样本数 / 预测为正类样本数
• 召回率 = 预测中真正的正类样本数 / 样本中的正类样本数

b. 合理值区间

精确率和召回率的取值范围也在 0% 到 100% 之间。一般来说，需要根据具体问题来权衡精确率和召回率的重要性，没有固定的合理值区间。

c. 应用场景

在信息检索、疾病诊断等场景中非常重要。例如，在垃圾邮件过滤中，需要在保证较高精确率的同时，尽可能提高召回率，以确保不会错过重要的邮件。这里需要注意要分清业务目标是偏向于召回率还是精确率。因为实际场景中两者的高取值往往不可兼得。

d. 优缺点

• 优点：能够更细致地评估模型在不同方面的性能，特别是在处理类别不平衡问题时比准确率更有价值。
• 缺点：单独使用精确率或召回率可能会忽略另一方面的性能，需要结合起来综合考虑。

3. F1 值

a. 用法

• F1 值是精确率和召回率的调和平均数，它综合考虑了精确率和召回率的平衡。
• 计算公式为：F1 = 2 × 精确率 × 召回率 / （精确率 + 召回率）。

b. 合理值区间

同精确率和召回率一样，F1 值的取值范围在 0% 到 100% 之间。一般来说，F1 值越高越好。

c. 应用场景

常用于需要同时考虑精确率和召回率的场景，作为一个综合指标来评估模型性能。

d. 优缺点

• 优点：平衡了精确率和召回率，能够更全面地反映模型的性能。
• 缺点：仍然不能完全涵盖所有的性能方面，可能在某些特殊情况下不够准确。

4. AUC值

a. 定义及计算方法

定义：AUC 值衡量的是分类器区分正例和负例的能力。它通过绘制不同阈值下的真正例率（True Positive Rate，TPR）与假正例率（False Positive Rate，FPR）的关系曲线，计算曲线下的面积得到。

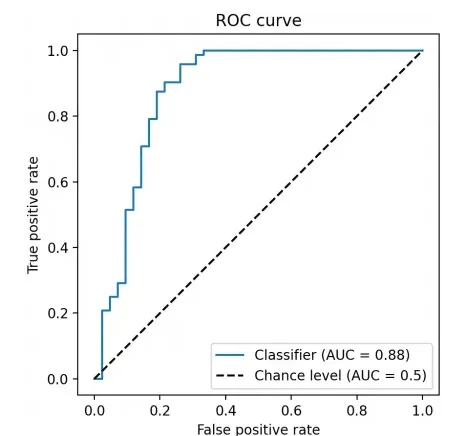
计算公式：AUC 的计算通常使用积分的方法，由于 ROC 曲线通常是阶梯状的，实际计算中可以通过近似求和的方式进行。对于一系列不同阈值下的 TPR 和 FPR 值，可以通过梯形法则近似计算 AUC 值。

b. 用法

• 评估分类器性能：AUC 值越大，说明分类器在不同阈值下区分正例和负例的能力越强。一般来说，AUC 值在 0.5 到 1 之间，随机猜测的分类器的 AUC 值为 0.5，完美分类器的 AUC 值为 1。
• 比较不同分类器：可以通过比较不同分类器的 AUC 值来选择性能更好的模型。在实际应用中，常常会尝试多种不同的分类算法或调整模型参数，然后比较它们的 AUC 值来确定最佳的模型。
• 确定最佳阈值：通过观察 ROC 曲线和 AUC 值，可以帮助确定分类器的最佳阈值。在不同的应用场景中，可能需要根据具体的业务需求来平衡真正例率和假正例率，AUC 值可以为选择合适的阈值提供参考。

c. 合理值区间

AUC 值的合理值区间为 0.5 到 1。越接近 1 表示分类器性能越好，0.5 表示分类器性能与随机猜测相当。一般来说，AUC 值大于 0.7 被认为是一个较好的分类器性能，具体的合理值还需要根据具体问题和应用场景来确定。

d. 应用场景

• 医学诊断：在疾病诊断中，评估不同的诊断方法或生物标志物的分类性能。例如，通过比较不同的血液检测指标对某种疾病的诊断能力，选择 AUC 值较高的指标用于临床诊断。
• 金融风险评估：用于评估信用风险模型、欺诈检测模型等的性能。例如，在信用评分中，通过 AUC 值来衡量模型区分违约客户和正常客户的能力，以降低信用风险。
• 图像识别：在图像分类任务中，比较不同的深度学习模型或算法的性能。AUC 值可以作为一个客观的指标来评估模型对不同类别的区分能力，帮助选择最佳的模型架构和参数。

e. 优缺点

优点：

• 不受类别不平衡的影响：与准确率等指标不同，AUC 值对正负例样本比例的变化不敏感，特别适用于类别不平衡的问题。
• 综合衡量分类性能：AUC 值考虑了不同阈值下的分类性能，能够综合反映分类器在各种情况下区分正例和负例的能力。
• 直观易懂：AUC 值的含义比较直观，容易理解和解释，便于与业务人员沟通和决策。

缺点：

• 计算相对复杂：AUC 值的计算需要绘制 ROC 曲线，对于大规模数据集或复杂模型，计算可能比较耗时。
• 不能直接反映具体的错误率：AUC 值只能反映分类器的整体性能，不能直接给出具体的错误率或准确率等指标，在某些情况下可能需要结合其他指标进行综合评估。

5. KS值

a. 用法

计算 KS 值通常需要将样本按照预测为正例的概率从高到低排序，然后分别计算每个概率分位点上的累计正例占比和累计负例占比，两者之差的最大值即为 KS 值。

KS 值反映了模型对正例和负例的区分程度，值越大表示模型的区分能力越强。

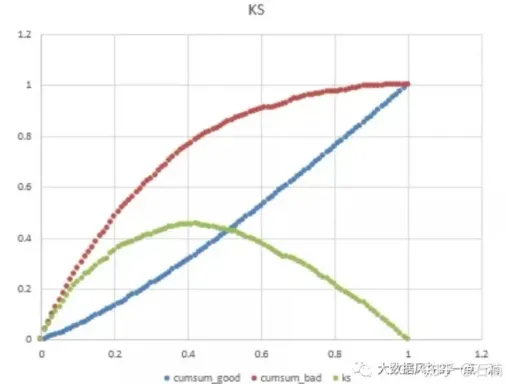
b. 合理值区间

一般来说，KS 值在 0.2 以下表示模型区分能力较弱；0.2 – 0.4 之间表示模型有一定区分能力；0.4 以上表示模型区分能力较强。但具体的合理值区间会因不同的业务场景和数据特点而有所差异。

c. 应用场景

• 信用评分：在金融领域，用于评估信用风险模型对违约客户和正常客户的区分能力。通过 KS 值可以确定模型在不同风险等级上的区分效果，帮助金融机构制定合理的信贷政策。
• 欺诈检测：在保险、电商等行业，用于检测欺诈行为。KS 值可以衡量模型对欺诈交易和正常交易的区分程度，提高欺诈检测的准确性。
• 营销响应预测：在市场营销中，预测客户对营销活动的响应概率。KS 值可以评估模型对响应客户和非响应客户的区分能力，优化营销资源的分配。

d. 优缺点

优点：

• 直观反映模型区分能力：KS 值能够直观地显示模型对正例和负例的区分程度，易于理解和解释。
• 不受样本比例影响：与准确率等指标不同，KS 值不受正负例样本比例的影响，适用于不平衡数据集。
• 可用于选择最优模型：通过比较不同模型的 KS 值，可以选择区分能力最强的模型。

缺点：

• 不能全面评估模型性能：KS 值只关注模型的区分能力，不能反映模型的准确性、稳定性等其他方面的性能。
• 对阈值敏感：KS 值的计算依赖于阈值的选择，不同的阈值可能会导致不同的 KS 值，需要谨慎选择阈值。
• 不能直接用于决策：KS 值只是一个评估指标，不能直接用于业务决策，需要结合实际业务情况进行综合考虑。

6. 均方误差（Mean Squared Error，MSE）和均方根误差（Root Mean Squared Error，RMSE）

a. 用法

这两个指标主要用于回归问题，衡量模型预测值与真实值之间的差异。

MSE 是预测值与真实值之差的平方的平均值。RMSE 是 MSE 的平方根。

计算公式为：MSE = Σ(预测值 – 真实值)^2 / 样本数；RMSE = √MSE。

b. 合理值区间

MSE 和 RMSE 的值越小越好，没有固定的合理值区间，具体取决于问题的规模和数据的特性。

c. 应用场景

在房价预测、销售预测等回归问题中广泛使用。

d. 优缺点

优点：能够直观地反映预测值与真实值之间的差异程度。

缺点：对异常值比较敏感，可能会因为少数异常值而导致指标值大幅上升。

7. 平均绝对误差（Mean Absolute Error，MAE）

a. 用法

MAE 也是用于回归问题的指标，它计算预测值与真实值之差的绝对值的平均值。

计算公式为：MAE = Σ| 预测值 – 真实值 | / 样本数。

b. 合理值区间

同 MSE 和 RMSE 一样，MAE 的值越小越好，具体合理值取决于问题的具体情况。

c. 应用场景

常用于回归问题，与 MSE 和 RMSE 一起作为评估模型性能的指标。

d. 优缺点

优点：对异常值相对不那么敏感，能够更稳健地反映模型的平均误差。

缺点：可能不如 MSE 和 RMSE 那样能突出较大的误差。

8. R² 系数（Coefficient of Determination）

a. 用法

R² 系数用于衡量回归模型对数据的拟合程度。它表示模型解释的方差占总方差的比例。

计算公式为：R² = 1 – Σ(真实值 – 预测值)^2 / Σ(真实值 – 平均值)^2。

b. 合理值区间

R² 的取值范围在 0% 到 100% 之间，越接近 100% 表示模型拟合越好。

c. 应用场景

在回归分析中，用于评估模型的整体性能和解释能力。

d. 优缺点

优点：能够直观地反映模型对数据的拟合程度，解释性较强。

缺点：可能会受到数据量和特征选择的影响，在某些情况下可能会出现过拟合导致 R² 值过高的情况。

9. PSI指标

a. 用法

首先将数据分为两组，通常是训练集和验证集（或不同时间段的数据）。

对于每个分箱区间（可以根据特征值进行等频分箱等），计算该区间内训练集样本的占比和验证集样本的占比。

然后计算每个分箱区间的 PSI 值，公式为：PSI = sum ((实际占比 – 预期占比) * ln (实际占比 / 预期占比))。

最后将各个分箱区间的 PSI 值相加得到总体的 PSI 值。

PSI 值反映了两个数据集在各个分箱区间上的分布差异程度。如果 PSI 值接近 0，说明两个数据集的分布相似，模型比较稳定；如果 PSI 值较大，则说明两个数据集的分布有较大差异，模型可能不稳定。

b. 合理值区间

一般认为 PSI 值在 0.1 以下表示模型稳定性很高；0.1 – 0.25 表示模型有一定程度的变化，但仍相对稳定；超过 0.25 则表示模型稳定性较差，需要进一步分析和调整。

c. 应用场景

模型监控

在模型上线后，持续监控模型的稳定性。通过比较不同时间段的数据在模型上的表现，计算 PSI 值来判断模型是否随着时间发生了较大变化。如果 PSI 值超出合理范围，可能需要重新评估和调整模型。

例如，在金融领域的信用评分模型中，每月对新数据和历史数据进行 PSI 计算，以确保模型在不同月份的稳定性。

变量筛选

在特征工程中，可以计算每个特征的 PSI 值，来判断该特征在不同数据集上的稳定性。如果某个特征的 PSI 值较大，说明该特征的分布不稳定，可能不适合作为模型的输入变量。

例如，在电商销售预测模型中，对不同商品属性特征进行 PSI 计算，筛选出稳定性较高的特征用于建模。

数据漂移检测

检测数据是否发生了漂移，即数据的分布是否发生了变化。如果数据发生了漂移，可能会影响模型的性能。通过计算 PSI 值可以及时发现数据漂移现象，采取相应的措施，如重新训练模型或调整数据预处理方法。

例如，在工业生产过程中，对传感器数据进行 PSI 计算，检测生产过程是否发生了变化，以便及时调整生产参数。

d. 优缺点

优点：

• 直观反映模型或数据的稳定性：PSI 值能够清晰地量化两个数据集之间的分布差异，帮助用户快速判断模型或数据的稳定性。
• 易于计算和解释：PSI 的计算方法相对简单，结果易于理解，不需要复杂的统计知识。
• 可用于不同类型的数据：适用于各种类型的数据，包括连续变量和离散变量。

缺点：

• 对分箱敏感：PSI 值的计算结果受到分箱方法和分箱数量的影响。不同的分箱方式可能会导致不同的 PSI 值，需要谨慎选择分箱方法。
• 不能完全反映模型性能：PSI 值主要关注数据分布的变化，不能全面反映模型的准确性、召回率等性能指标。在某些情况下，即使 PSI 值较低，模型的性能也可能不理想。
• 不能定位问题根源：当 PSI 值较大时，只能表明模型或数据存在问题，但不能直接指出问题的具体原因。需要进一步分析数据和模型，才能确定问题的根源。

10. IV指标

IV（Information Value）即信息价值，是在信用评分、风险评估等领域常用的评估指标。

a. 定义及计算方法

IV 值衡量了某个特征对目标变量的预测能力。其计算公式如下：

b. 用法

特征筛选：IV 值可以帮助确定哪些特征对目标变量有较强的预测能力。通常，IV 值大于一定阈值（如 0.02 或 0.1，具体根据实际情况确定）的特征被认为是有价值的，可以保留用于建模；IV 值较低的特征可能对模型的贡献较小，可以考虑删除。

比较不同特征的重要性：通过比较各个特征的 IV 值，可以判断哪些特征在预测目标变量时更为重要。IV 值越高，说明该特征与目标变量的关联越强。

c. 合理值区间

一般来说，IV 值的范围在 0 到无穷大之间。

当 IV 值接近 0 时，表示该特征几乎没有预测能力。

当 IV 值在 0.02 到 0.1 之间时，特征具有一定的预测能力。

当 IV 值大于 0.3 时，特征通常具有很强的预测能力，但也可能存在过拟合的风险。

d. 应用场景

• 信用评分模型：在构建信用评分模型时，用于筛选对客户信用风险有显著影响的特征，如收入、负债比、信用历史等。通过计算这些特征的 IV 值，可以确定哪些特征对客户违约风险的预测能力最强，从而提高模型的准确性。
• 营销响应模型：在营销活动中，预测客户对营销活动的响应概率。例如，通过分析客户的年龄、性别、消费习惯等特征的 IV 值，可以确定哪些客户特征与营销响应有较强的关联，从而有针对性地进行营销活动，提高营销效果。
• 风险评估：在金融、保险等领域，用于评估客户的风险水平。例如，在保险业务中，通过分析客户的职业、健康状况、驾驶记录等特征的 IV 值，可以确定哪些因素对客户的理赔风险有较大影响，从而制定合理的保险费率。

e. 优缺点

优点：

• 能够有效地衡量特征的预测能力，为特征筛选和模型构建提供重要依据。
• 计算相对简单，易于理解和应用。
• 可以比较不同特征之间的重要性，帮助建模者聚焦于关键特征。

缺点：

• IV 值的计算依赖于数据的分组，不同的分组方式可能会导致不同的 IV 值。
• 对于极端值或异常值较为敏感，可能会影响 IV 值的准确性。
• IV 值只能衡量单个特征与目标变量的关联，不能考虑特征之间的交互作用。

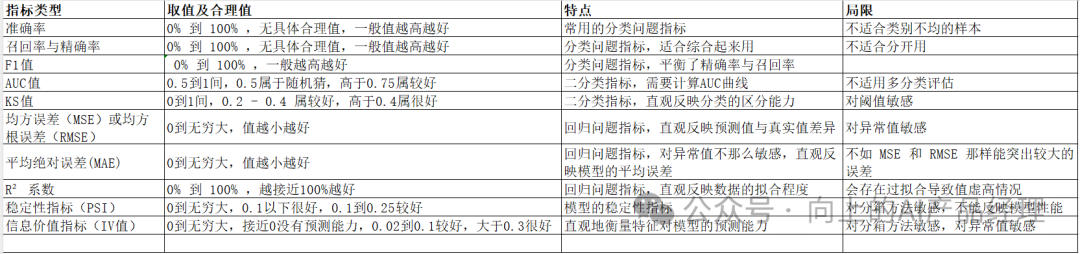
11. 指标总结

以上模型介绍的指标总结如下：