在面试中，Fermi Problem往往能间接反映出一个人的综合素质。

你是否有在面试中遇到过这样的奇怪问题？

• 一个正常成年人有多少根头发？
• 北京有多少个加油站？
• 胡同口的煎饼摊子一年能卖多少个煎饼？
• 一辆公交车里能装下多少个乒乓球？
  …

在产品和市场的面试或者工作中，我们常常会遇到对于对某项指标的估算问题。有些是对某个市场的估算，有些是对行业未来预测。

需要被考察者在有限的时间，有限的资源的情况下，对问题进行分析，最终得出一个经得起推敲的答案。

这类问题英文称之为Fermi problem。即「费米问题」

关于Fermi problem，维基百科的解释是：

In physics or engineering education, a Fermi problem, Fermi quiz, Fermi question, Fermi estimate, or order estimation is an estimation problem designed to teach dimensional analysis, approximation, and such a problem is usually a back-of-the-envelope calculation.

正如这段引用所说，「费米问题」能够锻炼一个人的多方位思考分析能力。你不但需要有不错的思维逻辑，同时需要有较为广泛的知识面涉及。所以在面试中，Fermi Problem往往能间接反映出一个人的综合素质。

同样地，在日常工作中。估算同样发挥着它的作用。大到资本市场对青睐的公司或行业的潜力预测，小到某场运营活动的前期市场调研。学会估算能让我们在做决定时不至于完全摸不着头脑。

解决此类问题的方法有很多种。个人推荐 Top-down，bottom-up法则。

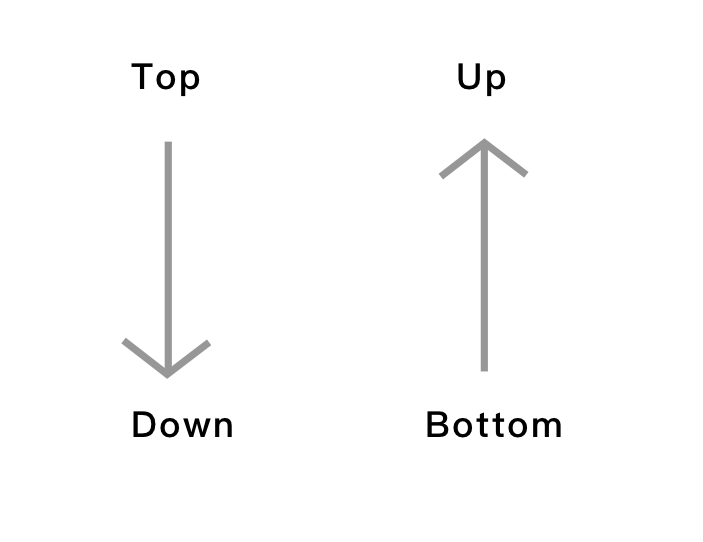
这个法则的中心思想是：

• 首先，分别从两个角度展开。一是先从宏观层面，由上层往下推。二是由某个点横向切入，反推上去。
• 其次，拿两次推测得到的结果进行对比，如果相差在一定的范围内。那么我们认为这个结论是可以信任的。
• 最后，为了使结论更具有客观性。我们需要补充上可能出现「误差」的地方，以及误差对结果的影响。

理论性的东西听起来总是很拗口，举个例子来看：

假如需估算深圳市丰田汽车的数量？

先top-down分析：

• 假设已知深圳市全市共有机动车300万辆
• 在深圳市几个车流密集区域采样，记录每100辆车中丰田车的占比，取平均占比。假如为25%
• 300万×25%=75万辆

再bottom-up分析：

假设已知深圳全市有「特斯拉」8万辆 在某地多点采样得出，在每100辆汽车车中，「特斯拉」车的占比为2%，丰田车的占比为20%。

8万／2*20%=80万辆

不难看出，以上两个分析的出发角度是不同的。前者从宏观往下，取得平均占比后，乘以总数，得到丰田车的数量。后者从微观往上，以另一款汽车「特斯拉」作为切入，反推丰田车的数量。

得到75万，80万的这两个数字，差距在一定的范围内，则认为这个数据是可以取信的。

最后，我们还需要进行误差分析。

在对丰田汽车采样的时候，若只取了口岸附近的车流密集区，则占比有可能偏高（香港牌的保姆车绝大多数是丰田埃尔法：http://mini.eastday.com/mobile/161119115415503.html）

2.在对特斯拉进行采样时，若取样地点是「特斯拉充电桩」附近，同样也会造成数据偏高的情况。

（深圳充电桩分布）

当然这里对于误差的分析，可以再多些维度。比如日本企业聚集区，特斯拉某次大促后的时间点，采样的时间是工作日还说周末等都可能是造成误差的因素，这里就不再展开了。有了估算数据和误差分析，基本上一个费米问题的解答就算是OK了。

「费米问题」又被称作理科生的脑筋急转弯。这里附上来自马里兰州大学的费米问题库http://www.physics.umd.edu/perg/fermi/fermi.htm。

内容涵盖了理工科多个领域。感兴趣的朋友可以去看看。

此类问题是可以通过训练找到方法等。通过思考此类问题，对于锻炼思维的开阔性，有不错的帮助。

最后，留下一个问题：

如果让你来估算「北京某胡同口的煎饼摊一年能卖出多少个煎饼？」你的思路是什么？

可以把你的思路留言在文末。我们一起探讨探讨吧！

#专栏作家#

Earon，微信公众号：earonpm，人人都是产品经理专栏作家。爱码字、喜欢尝试新事物、产品路上刚起步的新人，关注移动产品。怀谦卑之心，渴望交流之中共同成长。

本文原创发布于人人都是产品经理，未经许可，不得转载。